Galois group
The automorphism group of a Galois extension  of a field
of a field  , i.e. the group of all automorphisms of the field
, i.e. the group of all automorphisms of the field  leaving the elements of the subfield
leaving the elements of the subfield  fixed. The group is denoted by
fixed. The group is denoted by  or by
or by  . The field of invariants
. The field of invariants  coincides with the field
coincides with the field  . If
. If  is the splitting field of a polynomial
is the splitting field of a polynomial  over
over  , the Galois group
, the Galois group  is also called the Galois group of the polynomial
is also called the Galois group of the polynomial  . These groups are important in the Galois theory of algebraic equations. The computation of the Galois groups for extensions of algebraic number fields is one of the fundamental tasks of algebraic number theory. Finding Galois extensions with an Abelian Galois group (Abelian extensions) is a part of class field theory. Galois groups of algebraic function fields are also a subject of algebraic geometry.
. These groups are important in the Galois theory of algebraic equations. The computation of the Galois groups for extensions of algebraic number fields is one of the fundamental tasks of algebraic number theory. Finding Galois extensions with an Abelian Galois group (Abelian extensions) is a part of class field theory. Galois groups of algebraic function fields are also a subject of algebraic geometry.
Let  be a field and let
be a field and let  be a finite subgroup of the automorphism group of
be a finite subgroup of the automorphism group of  ;
;  will then be a Galois extension of the field of invariants
will then be a Galois extension of the field of invariants  , and the Galois group of this extension is isomorphic to
, and the Galois group of this extension is isomorphic to  ; moreover, the degree of the extension,
; moreover, the degree of the extension,  , is equal to the order of
, is equal to the order of  .
.
The fundamental result on Galois groups is the following theorem, which is sometimes called the main theorem on Galois extensions or the theorem on Galois correspondence. If  is a Galois extension of finite degree of a field
is a Galois extension of finite degree of a field  , then there exists a one-to-one correspondence between all subgroups
, then there exists a one-to-one correspondence between all subgroups  of the Galois group
of the Galois group  and all subfields
and all subfields  of
of  that contain
that contain  , and the
, and the  and
and 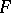 corresponding to each other are such that
corresponding to each other are such that  is the field of invariants of
is the field of invariants of  and
and  is the Galois group of
is the Galois group of  (cf. Galois correspondence). This theorem has numerous analogues in many mathematical theories, and can be generalized to extensions of infinite degree (cf. Galois topological group). There exists a generalization of the concept of a Galois group to extensions of arbitrary commutative rings, schemes (cf. Fundamental group), and also to the case of extensions of skew-fields.
(cf. Galois correspondence). This theorem has numerous analogues in many mathematical theories, and can be generalized to extensions of infinite degree (cf. Galois topological group). There exists a generalization of the concept of a Galois group to extensions of arbitrary commutative rings, schemes (cf. Fundamental group), and also to the case of extensions of skew-fields.
References
| [1] | N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Springer (1989) pp. Chapt. 1–3 (Translated from French) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1984) |
| [3] | M.M. Postnikov, "Fundamentals of Galois theory" , Noordhoff (1962) (Translated from Russian) |
| [4] | N. Jacobson, "The theory of rings" , Amer. Math. Soc. (1943) |
Comments
A Galois group can be endowed with the Krull topology, making it a topological group. This topology is discrete if and only if the group is finite. For the Galois correspondence in the case of infinite Galois groups see Galois topological group.
Galois group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_group&oldid=18702