Difference between revisions of "Galois field"
(Importing text file) |
(start conversion) |
||
| Line 3: | Line 3: | ||
A field with a finite number of elements. First considered by E. Galois [[#References|[1]]]. | A field with a finite number of elements. First considered by E. Galois [[#References|[1]]]. | ||
| − | The number of elements of any | + | The number of elements of any finite field is a power $p^n$ of a prime number $p$, which is the [[Characteristic of a field|characteristic]] of this field. For any prime number $p$ and any natural number $n$ there exists a (unique up to an isomorphism) field of $p^n$ elements. It is denoted by $\mathrm{GF}(p^n)$ or by $\mathbb{F}_{p^n}$. The field $\mathrm{GF}(p^m)$ contains the field $\mathrm{GF}(p^n)$ as a subfield if and only if $m$ is divisible by $n$. In particular, any field $\mathrm{GF}(p^n)$ contains the field $\mathrm{GF}(p)$, which is called the [[prime field]] of characteristic $p$. The field $\mathrm{GF}(p)$ is isomorphic to the field $\mathbb{Z}/p\mathbb{Z}$ of residue classes of the ring of integers modulo $p$. In any fixed [[Algebraic closure|algebraic closure]] $\Omega$ of $\mathrm{GF}(p)$ there exists exactly one subfield $\mathrm{GF}(p^n)$ for each $n$. The correspondence $n \leftrightarrow \mathrm{GF}(p^n)$ is an isomorphism between the lattice of natural numbers with respect to division and the lattice of finite algebraic extensions (in $\Omega$) of $\mathrm{GF}(p)$ with respect to inclusion. The lattice of finite algebraic extensions of any Galois field within its fixed algebraic closure is such a lattice. |
The algebraic extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314026.png" /> is simple, i.e. there exists a primitive element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314027.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314028.png" />. Such an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314029.png" /> will be any root of any irreducible polynomial of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314030.png" /> from the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314031.png" />. The number of primitive elements of the extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314032.png" /> equals | The algebraic extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314026.png" /> is simple, i.e. there exists a primitive element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314027.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314028.png" />. Such an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314029.png" /> will be any root of any irreducible polynomial of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314030.png" /> from the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314031.png" />. The number of primitive elements of the extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043140/g04314032.png" /> equals | ||
Revision as of 06:37, 31 August 2013
finite field
A field with a finite number of elements. First considered by E. Galois [1].
The number of elements of any finite field is a power $p^n$ of a prime number $p$, which is the characteristic of this field. For any prime number $p$ and any natural number $n$ there exists a (unique up to an isomorphism) field of $p^n$ elements. It is denoted by $\mathrm{GF}(p^n)$ or by $\mathbb{F}_{p^n}$. The field $\mathrm{GF}(p^m)$ contains the field $\mathrm{GF}(p^n)$ as a subfield if and only if $m$ is divisible by $n$. In particular, any field $\mathrm{GF}(p^n)$ contains the field $\mathrm{GF}(p)$, which is called the prime field of characteristic $p$. The field $\mathrm{GF}(p)$ is isomorphic to the field $\mathbb{Z}/p\mathbb{Z}$ of residue classes of the ring of integers modulo $p$. In any fixed algebraic closure $\Omega$ of $\mathrm{GF}(p)$ there exists exactly one subfield $\mathrm{GF}(p^n)$ for each $n$. The correspondence $n \leftrightarrow \mathrm{GF}(p^n)$ is an isomorphism between the lattice of natural numbers with respect to division and the lattice of finite algebraic extensions (in $\Omega$) of $\mathrm{GF}(p)$ with respect to inclusion. The lattice of finite algebraic extensions of any Galois field within its fixed algebraic closure is such a lattice.
The algebraic extension 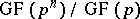 is simple, i.e. there exists a primitive element
is simple, i.e. there exists a primitive element  such that
such that 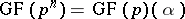 . Such an
. Such an 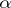 will be any root of any irreducible polynomial of degree
will be any root of any irreducible polynomial of degree  from the ring
from the ring 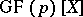 . The number of primitive elements of the extension
. The number of primitive elements of the extension  equals
equals
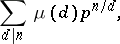 |
where  is the Möbius function. The additive group of the field
is the Möbius function. The additive group of the field 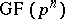 is naturally endowed with the structure of an
is naturally endowed with the structure of an  -dimensional vector space over
-dimensional vector space over  . As a basis one may take
. As a basis one may take  . The non-zero elements of
. The non-zero elements of 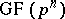 form a multiplicative group,
form a multiplicative group, 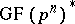 , of order
, of order  , i.e. each element of
, i.e. each element of 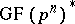 is a root of the polynomial
is a root of the polynomial 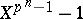 . The group
. The group 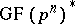 is cyclic, and its generators are the primitive roots of unity of degree
is cyclic, and its generators are the primitive roots of unity of degree 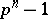 , the number of which is
, the number of which is 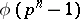 , where
, where  is the Euler function. Each primitive root of unity of degree
is the Euler function. Each primitive root of unity of degree 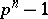 is a primitive element of the extension
is a primitive element of the extension  , but the converse is not true. More exactly, out of the
, but the converse is not true. More exactly, out of the
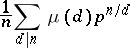 |
irreducible unitary polynomials of degree  over
over 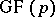 there are
there are 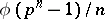 polynomials of which the roots are generators of
polynomials of which the roots are generators of 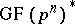 .
.
The set of elements of 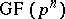 coincides with the set of roots of the polynomial
coincides with the set of roots of the polynomial 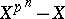 in
in  , i.e.
, i.e. 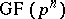 is characterized as the subfield of elements from
is characterized as the subfield of elements from  that are invariant with respect to the automorphism
that are invariant with respect to the automorphism 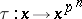 , which is known as the Frobenius automorphism. If
, which is known as the Frobenius automorphism. If 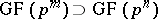 , the extension
, the extension 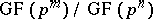 is normal (cf. Extension of a field), and its Galois group
is normal (cf. Extension of a field), and its Galois group 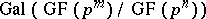 is cyclic of order
is cyclic of order  . The automorphism
. The automorphism  may be taken as the generator of
may be taken as the generator of 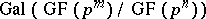 .
.
References
| [1] | E. Galois, "Écrits et mémoires d'E. Galois" , Gauthier-Villars (1962) |
| [2] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [3] | N.G. [N.G. Chebotarev] Tschebotaröw, "Grundzüge der Galois'schen Theorie" , Noordhoff (1950) (Translated from Russian) |
| [4] | N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Springer (1989) pp. Chapt. 1–3 (Translated from French) |
Galois field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_field&oldid=12669