Gödel interpretation
of intuitionistic arithmetic
A translation of formulas of intuitionistic arithmetic into formulas of the type 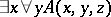 , where
, where  ,
,  and
and  are variables of various finite types. Provable formulas of arithmetic are translated into provable formulas of a quantifier-free theory of finite types. Thus, this translation reduces the consistency of intuitionistic arithmetic (and hence of classical arithmetic) to that of such a theory of finite types, as was Gödel's original aim.
are variables of various finite types. Provable formulas of arithmetic are translated into provable formulas of a quantifier-free theory of finite types. Thus, this translation reduces the consistency of intuitionistic arithmetic (and hence of classical arithmetic) to that of such a theory of finite types, as was Gödel's original aim.
This type theory, call it 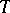 , has an infinite list of variables of each type
, has an infinite list of variables of each type 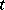 : 1) a type
: 1) a type  (the type of natural numbers); and 2) if
(the type of natural numbers); and 2) if 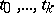 are types, then
are types, then 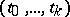 is a type (the type of functions which take
is a type (the type of functions which take 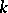 arguments of types
arguments of types 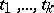 , respectively, into a value of type
, respectively, into a value of type 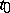 ). The language
). The language 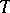 contains terms of various types: a variable
contains terms of various types: a variable 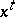 of type
of type 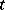 is a term of type
is a term of type 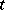 , 0 is a term of type 0, and the symbol
, 0 is a term of type 0, and the symbol  which denotes the function of adding one to a natural number is a term of type
which denotes the function of adding one to a natural number is a term of type 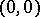 . The remaining terms are formed by generation laws: Church
. The remaining terms are formed by generation laws: Church 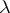 -abstraction and primitive recursion for functions of arbitrary type. The atomic formulas of
-abstraction and primitive recursion for functions of arbitrary type. The atomic formulas of 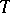 are equalities
are equalities 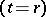 , where
, where 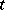 ,
,  are terms of type zero. The formulas of
are terms of type zero. The formulas of 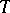 are obtained from atomic formulas with the aid of the logical connectives of propositional calculus:
are obtained from atomic formulas with the aid of the logical connectives of propositional calculus: 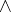 ,
,  ,
, 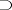 ,
,  . The postulates of
. The postulates of 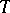 are the axioms and derivation rules of intuitionistic propositional calculus, equality axioms, the Peano axioms for 0 and
are the axioms and derivation rules of intuitionistic propositional calculus, equality axioms, the Peano axioms for 0 and  , equations of primitive recursion, the axiom of application of a function defined by
, equations of primitive recursion, the axiom of application of a function defined by 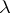 -abstraction, and, finally, the principle of mathematical induction, formulated as a derivation rule without the use of quantifiers.
-abstraction, and, finally, the principle of mathematical induction, formulated as a derivation rule without the use of quantifiers. 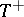 will denote the theory
will denote the theory 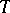 completed by quantifiers in variables of arbitrary type and corresponding logical axioms and derivation rules for quantifiers.
completed by quantifiers in variables of arbitrary type and corresponding logical axioms and derivation rules for quantifiers.
Gödel's interpretation translates any formula 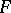 from
from 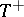 (i.e. any formula of intuitionistic arithmetic as well) into a formula of the type
(i.e. any formula of intuitionistic arithmetic as well) into a formula of the type
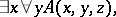 |
where 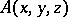 is a quantifier-free formula,
is a quantifier-free formula,  ,
, 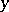 ,
,  are variables of different types, and
are variables of different types, and  is the set of all free variables of the formula
is the set of all free variables of the formula 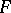 .
.
Let 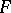 be a formula of intuitionistic arithmetic, and let
be a formula of intuitionistic arithmetic, and let 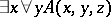 be its Gödel interpretation. If
be its Gödel interpretation. If 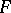 is deducible in formal intuitionistic arithmetic, it is possible to construct a term
is deducible in formal intuitionistic arithmetic, it is possible to construct a term 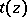 of
of 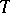 such that the formula
such that the formula 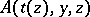 is deducible in
is deducible in 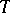 . Thus, the consistency of arithmetic is reduced to demonstrating the consistency of the quantifier-free theory
. Thus, the consistency of arithmetic is reduced to demonstrating the consistency of the quantifier-free theory 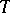 .
.
The intuitionistic semantics based on Gödel's interpretation is defined as follows: A formula 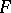 is considered to be true if it is possible to find a computable term
is considered to be true if it is possible to find a computable term  such that the quantifier-free formula
such that the quantifier-free formula 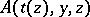 is true for any computable
is true for any computable  .
.
References
| [1] | K. Gödel, "Ueber eine bisher noch nicht benützte Erweiterung des finiten Standpunktes" Dialectica , 12 (1958) pp. 280–287 |
Comments
In the West this interpretation is commonly called the Dialectica interpretation.
References
| [a1] | E. Bishop, "Mathematics as a numerical language" A. Kino (ed.) J. Myhill (ed.) R.E. Vesley (ed.) , Intuitionism and Proof Theory , North-Holland (1970) pp. 53–71 |
| [a2] | A.S. Troelstra (ed.) , Metamathematical investigations , Lect. notes in math. , 344 , Springer (1973) pp. 230ff |
Gödel interpretation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%B6del_interpretation&oldid=15859