Gödel constructive set
Gödel constructible set, constructible set
A set arising in the process of constructing sets described below. Let 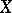 be a set and let
be a set and let 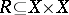 . Consider the first-order language
. Consider the first-order language 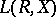 containing one
containing one  -place predicate symbol denoting the relation
-place predicate symbol denoting the relation 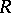 , and individual constants, denoting the elements of the set
, and individual constants, denoting the elements of the set 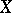 (for each
(for each 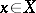 its constant is
its constant is  ). The statement "the formula f of the language LR, X is valid in the model M=X, R" is written:
). The statement "the formula f of the language LR, X is valid in the model M=X, R" is written:
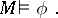 |
A set 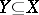 is called definable in the model
is called definable in the model 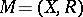 (or
(or 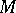 -definable) if there exists a formula
-definable) if there exists a formula 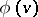 of
of 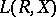 with one free variable
with one free variable  such that
such that
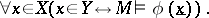 |
Let 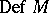 denote the set of all
denote the set of all 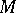 -definable sets. To each ordinal number
-definable sets. To each ordinal number 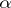 is associated the set
is associated the set 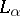 defined recursively by the relation
defined recursively by the relation
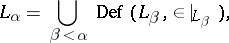 |
where 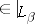 is the membership relation restricted to the set
is the membership relation restricted to the set 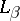 . Hence it follows that
. Hence it follows that
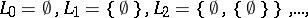 |
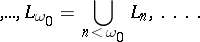 |
A set  is called constructible if there exists an ordinal number
is called constructible if there exists an ordinal number 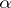 such that
such that 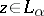 . The class of all constructible sets is denoted by
. The class of all constructible sets is denoted by 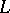 . In 1938, K. Gödel defined
. In 1938, K. Gödel defined 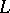 and introduced the following axiom of constructibility: Every set is constructible. On the basis of the axioms of
and introduced the following axiom of constructibility: Every set is constructible. On the basis of the axioms of 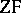 , he proved that in
, he proved that in 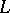 all axioms of
all axioms of 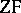 hold and also the axiom of constructibility, and that the axiom of choice and the generalized continuum hypothesis ( "for every ordinal number a one has 2a=a+ 1" ) follow in
hold and also the axiom of constructibility, and that the axiom of choice and the generalized continuum hypothesis ( "for every ordinal number a one has 2a=a+ 1" ) follow in 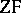 from the axiom of constructibility.
from the axiom of constructibility.
The class 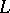 can also be characterized as the smallest class that is a model of
can also be characterized as the smallest class that is a model of 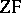 and contains all the ordinal numbers; there are other ways of defining
and contains all the ordinal numbers; there are other ways of defining 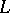 (see [2]–[4]). The relation
(see [2]–[4]). The relation 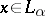 can be expressed by a formula in the language
can be expressed by a formula in the language 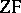 , which is moreover of a simple syntactic structure (a so-called
, which is moreover of a simple syntactic structure (a so-called 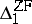 -formula, cf. ).
-formula, cf. ).
Some results relating to constructible sets. The set of constructible real numbers (cf. Constructive real number), that is, the set 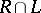 where
where 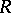 is the set of all real numbers, that is, sequences of zeros and ones, is a
is the set of all real numbers, that is, sequences of zeros and ones, is a 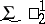 -set (see [5]). It has been shown that the axiom of constructibility implies the existence of a Lebesgue non-measurable set of real numbers of type
-set (see [5]). It has been shown that the axiom of constructibility implies the existence of a Lebesgue non-measurable set of real numbers of type 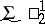 (see [6]), the negation of the Suslin hypothesis and the non-existence of measurable cardinal numbers (see [2]).
(see [6]), the negation of the Suslin hypothesis and the non-existence of measurable cardinal numbers (see [2]).
References
| [1a] | K. Gödel, "The consistency of the axiom of choice and of the generalized coninuum hypothesis" Proc. Nat. Acad. Sci. USA , 24 (1938) pp. 556–557 |
| [1b] | K. Gödel, "Consistency proof for the generalized coninuum hypothesis" Proc. Nat. Acad. Sci. USA , 25 (1939) pp. 220–224 |
| [2] | T.J. Jech, "Lectures in set theory: with particular emphasis on the method of forcing" , Lect. notes in math. , 217 , Springer (1971) |
| [3] | A. Mostowski, "Constructible sets with applications" , North-Holland (1969) |
| [4] | C. Karp, "A proof of the relative consistency of the continuum hypothesis" J. Crossley (ed.) , Sets, models and recursion theory , North-Holland (1967) pp. 1–32 |
| [5] | J.W. Addison, "Some consequences of the axiom of constructibility" Fund. Math. , 46 (1959) pp. 337–357 |
| [6] | P.S. Novikov, "On the non-contradictability of certain propositions of descriptive set theory" Trudy Mat. Inst. Steklov. , 38 (1951) pp. 279–316 (In Russian) |
| [7] | U. Felgner, "Models of 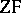 -set theory" , Springer (1971) -set theory" , Springer (1971) |
Comments
Concerning (the notation) 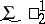 see Descriptive set theory.
see Descriptive set theory.
As a consequence of Gödel's findings, if the axioms of 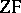 are non-contradictory, they remain so after addition of the axiom of choice and the generalized continuum hypothesis. This was the first relative consistency result for the theory
are non-contradictory, they remain so after addition of the axiom of choice and the generalized continuum hypothesis. This was the first relative consistency result for the theory 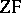 of any importance, to be surpassed only after a quarter of a century in 1963 by P. Cohen's forcing method. By forcing it is known that
of any importance, to be surpassed only after a quarter of a century in 1963 by P. Cohen's forcing method. By forcing it is known that 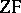 cannot prove the axiom of constructibility (unless it is contradictory). Most set theorists think there are no sufficient reasons to believe it to be true. Nevertheless,
cannot prove the axiom of constructibility (unless it is contradictory). Most set theorists think there are no sufficient reasons to believe it to be true. Nevertheless, 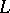 is an important subclass of the set-theoretic universe well worth investigating.
is an important subclass of the set-theoretic universe well worth investigating.
New results can be found in [a1], which is also a good introduction to constructibility. Reference [a2] contains (most of) the material touched upon in the main article.
References
| [a1] | K.J. Devlin, "Constructibility" , Springer (1984) |
| [a2] | T.J. Jech, "Set theory" , Acad. Press (1978) pp. 523ff (Translated from German) |
| [a3] | K. Kunen, "Set theory, an introduction to independence proofs" , North-Holland (1980) |
| [a4] | K. Gödel, "The consistency of the axiom of choice and of the generalized continuum hypothesis with the axioms of set theory" , Princeton Univ. Press (1940) |
| [a5] | K. Devlin, "Constructibility" J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) pp. 453–490 |
Gödel constructive set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%B6del_constructive_set&oldid=14011