Gâteaux variation
of a mapping 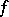 of a linear space
of a linear space 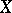 into a linear topological space
into a linear topological space 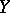
The limit, in the topology of 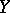 ,
,
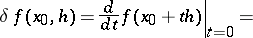 | (*) |
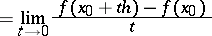 |
on the assumption that it exists for all 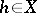 . This is how the first variation was introduced by R. Gâteaux in 1913–1914. This definition for functionals of the classical calculus of variations was given by J.L. Lagrange (cf. Variation of a functional).
. This is how the first variation was introduced by R. Gâteaux in 1913–1914. This definition for functionals of the classical calculus of variations was given by J.L. Lagrange (cf. Variation of a functional).
The expression 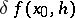 need not necessarily be a linear functional in
need not necessarily be a linear functional in 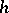 , but it is always a homogeneous function of the first degree in
, but it is always a homogeneous function of the first degree in 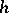 . The mapping
. The mapping 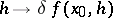 is also known as the Gâteaux differential or weak differential. Beginning with the work of P. Lévy, it is usual to stipulate the linearity and continuity of
is also known as the Gâteaux differential or weak differential. Beginning with the work of P. Lévy, it is usual to stipulate the linearity and continuity of 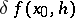 in
in 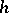 :
:
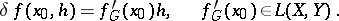 |
where 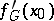 is called the Gâteaux derivative. Second, etc., variations are defined similarly to (*). See also Variation; Second variation; Differentiation of a mapping.
is called the Gâteaux derivative. Second, etc., variations are defined similarly to (*). See also Variation; Second variation; Differentiation of a mapping.
References
| [1a] | R. Gateaux, "Sur les fonctionnelles continues et les fonctionnelles analytiques" C.R. Acad. Sci. Paris Sér. I Math. , 157 (1913) pp. 325–327 |
| [1b] | R. Gateaux, "Fonctions d'une infinités des variables indépendantes" Bull. Soc. Math. France , 47 (1919) pp. 70–96 |
| [2] | P. Lévy, "Leçons d'analyse fonctionnelle" , Gauthier-Villars (1922) |
| [3] | P. Lévy, "Problèmes concrets d'analyse fonctionelle" , Gauthier-Villars (1951) |
Comments
References
| [a1] | M.S. Berger, "Nonlinearity and functional analysis" , Acad. Press (1977) |
Gâteaux variation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%A2teaux_variation&oldid=14647