Fundamental domain
of a discrete group 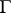 of transformations of a topological space
of transformations of a topological space 
A subset 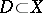 containing elements from all the orbits (cf. Orbit) of
containing elements from all the orbits (cf. Orbit) of  , with exactly one element from orbits in general position. There are various versions of the exact definition of a fundamental domain. Sometimes a fundamental domain is any subset belonging to a given
, with exactly one element from orbits in general position. There are various versions of the exact definition of a fundamental domain. Sometimes a fundamental domain is any subset belonging to a given 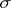 -algebra (for example, the Borel
-algebra (for example, the Borel 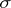 -algebra) and containing exactly one representative from each orbit. However, if
-algebra) and containing exactly one representative from each orbit. However, if 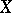 is a topological manifold, then a fundamental domain is usually a subset
is a topological manifold, then a fundamental domain is usually a subset  that is the closure of an open subset and is such that the subsets
that is the closure of an open subset and is such that the subsets  ,
, 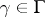 , have pairwise no common interior points and form a locally finite covering of
, have pairwise no common interior points and form a locally finite covering of 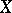 . For example, as a fundamental domain of the group of parallel translations of the plane
. For example, as a fundamental domain of the group of parallel translations of the plane 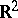 by integer vectors one can take the square
by integer vectors one can take the square
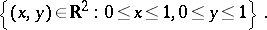 |
The choice of a fundamental domain is, as a rule, non-unique.
Comments
The chambers of the Weyl group 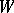 are examples of fundamental domains of
are examples of fundamental domains of 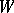 in its reflection representation.
in its reflection representation.
Fundamental domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fundamental_domain&oldid=13590