Functional derivative
Volterra derivative
One of the first concepts of a derivative in an infinite-dimensional space. Let 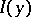 be some functional of a continuous function of one variable
be some functional of a continuous function of one variable  ; let
; let 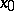 be some interior point of the segment
be some interior point of the segment  ; let
; let 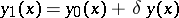 , where the variation
, where the variation 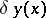 is different from zero in a small neighbourhood
is different from zero in a small neighbourhood 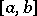 of
of 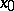 ; and let
; and let 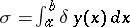 . The limit
. The limit
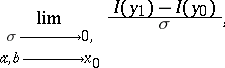 |
assuming that it exists, is called the functional derivative of 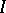 and is denoted by
and is denoted by 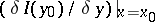 . For example, for the simplest functional of the classical calculus of variations,
. For example, for the simplest functional of the classical calculus of variations,
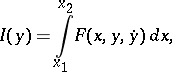 |
the functional derivative has the form
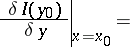 |
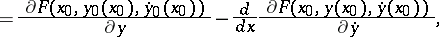 |
that is, it is the left-hand side of the Euler equation, which is a necessary condition for a minimum of 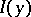 .
.
In theoretical questions the concept of a functional derivative has only historical interest, and in practice has been supplanted by the concepts of the Gâteaux derivative and the Fréchet derivative. But the concept of a functional derivative has been applied with success in numerical methods of the classical calculus of variations (see Variational calculus, numerical methods of).
Comments
The existence of the functional derivative of 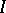 at
at 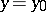 and
and 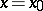 apparently means that the Fréchet derivative
apparently means that the Fréchet derivative 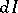 of
of 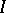 at
at 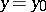 , which is a continuous linear form on the space of admissible infinitesimal variations
, which is a continuous linear form on the space of admissible infinitesimal variations  , is of the form
, is of the form 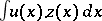 for some continuous function
for some continuous function  , so that it can be continuously extended to
, so that it can be continuously extended to 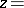 the
the  -function at
-function at 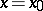 . In the example this happens only if
. In the example this happens only if 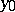 is twice continuously differentiable.
is twice continuously differentiable.
Functional derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Functional_derivative&oldid=47013