Function of bounded characteristic

in a domain 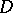of the complex plane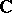

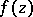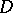A meromorphic function in that can be represented in 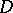as the quotient of two bounded analytic functions,

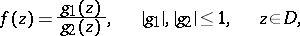(1)

is called a function of bounded type. The class most studied is the class 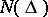of functions of bounded type in the unit disc 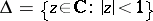: A meromorphic function in 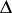belongs to 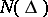if and only if its characteristic 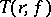is bounded (Nevanlinna's theorem):

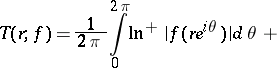(2)

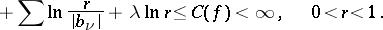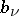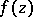Here the sum on the right-hand side is taken over all poles of with 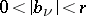, and each pole is taken as many times as its multiplicity; 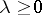is the multiplicity of the pole at the origin. Hence functions in the class 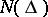are also called functions of bounded characteristic. The following sufficient condition is also of interest: If a meromorphic functio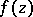n in 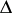does not take a set of values 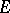of positive capacity, 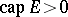, then .

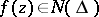The functions 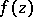in 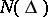have the following properties: 1) 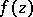has angular boundary values 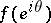, with 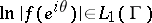, almost-everywhere on the unit circle 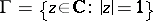; 2) if 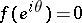on a set of points of 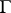of positive measure, then 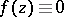; 3) a function 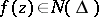is characterized by an integral representation of the form

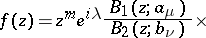(3)

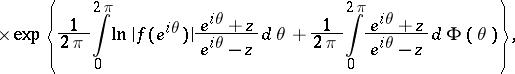where 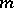is the integer such that 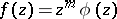, 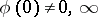; 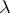is real; 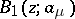and 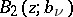are the Blaschke products taken over all zeros 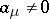and poles 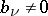of 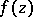inside 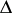, counted with multiplicity (cf. Blaschke product); and 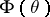is a singular function of bounded variation on 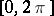with derivative equal to zero almost-everywhere.

The subclass 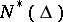of 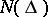consisting of all holomorphic functions 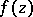in 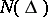is also of interest. A necessary and sufficient condition for a holomorphic function 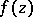to be in 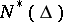is that it satisfies the following condition, deduced from (2),

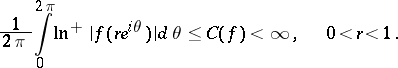(4)

For 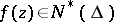one must have 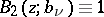, 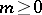in (3).

Condition (4) is equivalent to the requirement that the subharmonic function 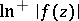has a harmonic majorant in the whole disc 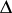. The condition in this form is usually taken to define the class 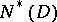of holomorphic functions on arbitrary domains 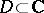: 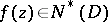if and only if 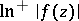has a harmonic majorant in the whole domain .

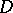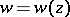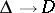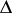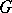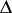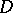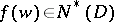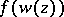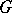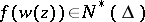Suppose that the function realizes a conformal universal covering mapping (i.e. a single-valued analytic function on that is automorphic with respect to the group of fractional-linear transformations of the disc onto itself corresponding to ). Then if and only if the composite function is automorphic relative to and . 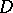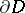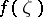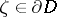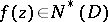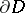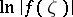If is a finitely-connected domain and if its boundary is rectifiable, then the angular boundary values , , of exist almost-everywhere on , and is summable with respect to harmonic measure on 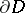(for more details see the survey [4]).

Now let 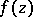, , 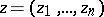, 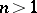be a holomorphic function of several variables on the unit polydisc 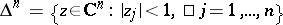, and let 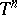be the skeleton of , 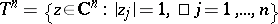. The class 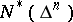of functions of bounded characteristic is defined by a condition generalizing (4):

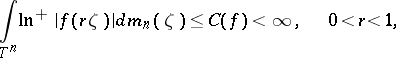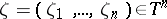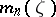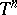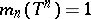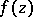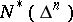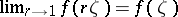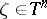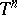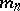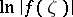where and is the normalized Haar measure on , . A holomorphic function in the class has radial boundary values , , almost-everywhere on with respect to Haar measure , and is summable on 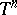. If the original definition (1) of a function of bounded type on 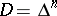is retained, then a function 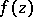of bounded type is a function of bounded characteristic, 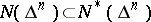. However, for 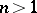there are functions 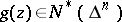that are not representable as the quotient of two bounded holomorphic functions (see [5]).

References

[1]	R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German)
[2]	A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian)
[3]	I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)
[4]	Itogi Nauk. Mat. Anal. 1963 (1965) pp. 5–80
[5]	W. Rudin, "Function theory in polydiscs" , Benjamin (1969)

Comments

One should not confuse the notion of "function of bounded type" as defined above with that of an entire function of bounded type. For this reason, functions 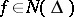are sometimes called functions of bounded form or have no special name at all, the class 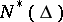being more important.