Fully-closed mapping
A continuous mapping  with the following property: For any point
with the following property: For any point 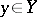 and for any finite family
and for any finite family  of open subsets of the space
of open subsets of the space  such that
such that  , the set
, the set  is open. Here
is open. Here  denotes the small image of the set
denotes the small image of the set  under the mapping
under the mapping  . Any fully-closed mapping is closed. The inequality
. Any fully-closed mapping is closed. The inequality  is valid for any fully-closed mapping
is valid for any fully-closed mapping  of a normal space
of a normal space  . For this reason, fully-closed mappings can be employed to isolate fairly wide classes of compacta with non-coinciding dimensions dim and ind. Moreover,
. For this reason, fully-closed mappings can be employed to isolate fairly wide classes of compacta with non-coinciding dimensions dim and ind. Moreover,  irrespective of the multiplicity of the mapping
irrespective of the multiplicity of the mapping  . Let
. Let  , let
, let 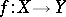 be a fully-closed mapping and let
be a fully-closed mapping and let 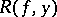 be the decomposition of
be the decomposition of  the elements of which are all pre-images
the elements of which are all pre-images  of the points, and all points of
of the points, and all points of  . Then, for a regular space
. Then, for a regular space  , the quotient space
, the quotient space  of
of  with respect to the decomposition
with respect to the decomposition  is also regular; this property is characteristic of fully-closed mappings in the class of closed mappings.
is also regular; this property is characteristic of fully-closed mappings in the class of closed mappings.
Fully-closed mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fully-closed_mapping&oldid=14852