Fubini-Study metric
The Hermitian metric on a complex projective space 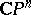 defined by the Hermitian scalar product in
defined by the Hermitian scalar product in 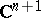 . It was introduced almost simultaneously by G. Fubini [1] and E. Study [2]. The Fubini–Study metric is given by the formula
. It was introduced almost simultaneously by G. Fubini [1] and E. Study [2]. The Fubini–Study metric is given by the formula
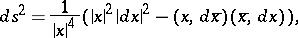 |
where  is the scalar product in
is the scalar product in 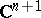 and
and 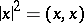 ; the distance
; the distance 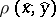 between the points
between the points  ,
, 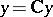 , where
, where 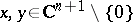 , is determined from the formula
, is determined from the formula
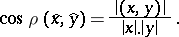 |
The Fubini–Study metric is Kählerian (and is even a Hodge metric); its associated Kähler form is
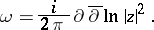 |
The Fubini–Study metric is, up to proportionality, the unique Riemannian metric on 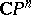 that is invariant under the unitary group
that is invariant under the unitary group 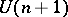 , which preserves the scalar product. The space
, which preserves the scalar product. The space 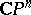 , endowed with the Fubini–Study metric, is a compact Hermitian symmetric space of rank 1. It is also called an elliptic Hermitian space.
, endowed with the Fubini–Study metric, is a compact Hermitian symmetric space of rank 1. It is also called an elliptic Hermitian space.
References
| [1] | G. Fubini, "Sulle metriche definite da una forme Hermitiana" Atti Istit. Veneto , 63 (1904) pp. 502–513 |
| [2] | E. Study, "Kürzeste Wege im komplexen Gebiet" Math. Ann. , 60 (1905) pp. 321–378 |
| [3] | E. Cartan, "Leçons sur la géometrie projective complexe" , Gauthier-Villars (1950) |
| [4] | S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962) |
| [5] | S.S. Chern, "Complex manifolds" , Univ. Recife (1959) |
Comments
Reference [a1] below is an extended and revised version of [4]. The Fubini–Study metric is extensively used in (multi-dimensional) complex analysis, [a2], [a3].
For Hodge and Kähler metrics cf. Kähler metric.
References
| [a1] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
| [a2] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
| [a3] | E.M. Chirka, "Complex analytic sets" , Kluwer (1989) (Translated from Russian) |
Fubini-Study metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fubini-Study_metric&oldid=22475