Frommer method
A method for investigating the singular points of an autonomous system of second-order ordinary differential equations
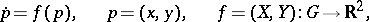 | (1) |
where  is an analytic or a sufficiently smooth function in the domain
is an analytic or a sufficiently smooth function in the domain 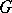 .
.
Suppose that  is a singular point of the system (1), that is,
is a singular point of the system (1), that is, 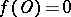 , and that
, and that 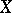 and
and 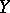 are analytic functions at
are analytic functions at 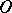 with no common analytic factor that vanishes at
with no common analytic factor that vanishes at 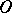 . The Frommer method enables one to find explicitly all
. The Frommer method enables one to find explicitly all 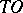 -curves of (1) — the semi-trajectories of the system joined to
-curves of (1) — the semi-trajectories of the system joined to  along a definite direction. Every
along a definite direction. Every 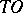 -curve of (1) not lying on the axis
-curve of (1) not lying on the axis 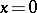 is an
is an 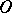 -curve of the equation
-curve of the equation
 | (2) |
(that is, can be represented near 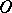 in the form
in the form
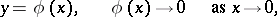 | (3) |
where 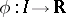 is a solution of (2),
is a solution of (2), 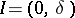 or
or 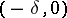 ,
, 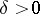 ,
,  or
or 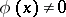 for every
for every 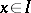 ), and conversely.
), and conversely.
Consider equation (2) first in the domain 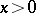 . If it is a simple Bendixson equation, that is, if it satisfies the conditions
. If it is a simple Bendixson equation, that is, if it satisfies the conditions
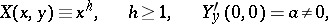 |
then it has a unique 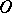 -curve in the domain
-curve in the domain 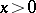 for
for 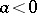 ; the domain
; the domain 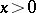 ,
, 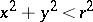 , where
, where  is a sufficiently small positive number, is a parabolic sector for
is a sufficiently small positive number, is a parabolic sector for 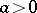 (cf. Sector in the theory of ordinary differential equations). Otherwise, to exhibit the
(cf. Sector in the theory of ordinary differential equations). Otherwise, to exhibit the 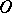 -curves of (2) in the domain
-curves of (2) in the domain 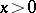 one applies the Frommer method. The basis for applying it is the fact that every
one applies the Frommer method. The basis for applying it is the fact that every  -curve (3) of equation (2),
-curve (3) of equation (2), 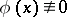 , has a completely determined asymptotic behaviour at
, has a completely determined asymptotic behaviour at  , namely, it can be represented in the form
, namely, it can be represented in the form
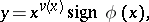 |
and admits a finite or infinite limit
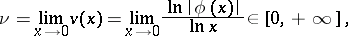 |
which is called its order of curvature at 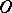 , and for
, and for 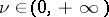 it also admits a finite or infinite limit
it also admits a finite or infinite limit
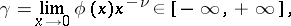 |
which is called its measure of curvature at 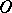 . Here the
. Here the 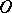 -curve
-curve 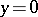 ,
, 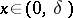 , is assigned the order of curvature
, is assigned the order of curvature 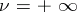 .
.
The first step in the Frommer method consists in the following. One uses algebraic means to calculate all possible orders of curvature  (there is always a finite number of them), and for each order
(there is always a finite number of them), and for each order 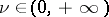 all possible measures of curvature for
all possible measures of curvature for 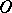 -curves of (2). On the basis of the general theorems of the method, one can elucidate the question of whether (2) has
-curves of (2). On the basis of the general theorems of the method, one can elucidate the question of whether (2) has 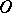 -curves with given possible order and measure of curvature, except for a finite number
-curves with given possible order and measure of curvature, except for a finite number 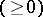 of so-called characteristic pairs
of so-called characteristic pairs 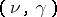 . For each of these
. For each of these 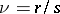 , where
, where  and
and  are natural numbers, and
are natural numbers, and 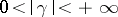 . Therefore the substitution
. Therefore the substitution 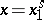 ,
, 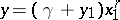 transforms (2) into a derived equation
transforms (2) into a derived equation 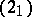 of the same form, turning the question of whether (2) has
of the same form, turning the question of whether (2) has 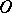 -curves with order of curvature
-curves with order of curvature  and measure of curvature
and measure of curvature 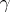 into the question of whether
into the question of whether 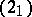 has
has 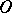 -curves in the domain
-curves in the domain 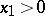 .
.
If (2) has no characteristic pairs or if each of its derived equations turns out to be a simple Bendixson equation, then all 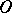 -curves of (2) in the domain
-curves of (2) in the domain 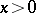 have been exhibited in the first step of the process. Otherwise one performs the second step — one studies, according to the plan of the first step, the derived equations that are not simple Bendixson equations. In doing this one arrives at derived equations of a second series, etc. At each stage the process, generally speaking, branches, but for a fixed equation (2) the number of branches of the process is finite and every branch terminates in a reduced equation which is either a simple Bendixson equation or has no characteristic pairs.
have been exhibited in the first step of the process. Otherwise one performs the second step — one studies, according to the plan of the first step, the derived equations that are not simple Bendixson equations. In doing this one arrives at derived equations of a second series, etc. At each stage the process, generally speaking, branches, but for a fixed equation (2) the number of branches of the process is finite and every branch terminates in a reduced equation which is either a simple Bendixson equation or has no characteristic pairs.
Thus, by means of a finite number of steps of the Frommer method one can exhibit all 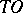 -curves of (1) in the domain
-curves of (1) in the domain 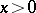 , along with their asymptotic behaviour at
, along with their asymptotic behaviour at 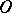 . Changing
. Changing  to
to 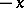 in (1) enables one to do the same for the domain
in (1) enables one to do the same for the domain 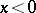 , and a direct verification enables one to establish whether the semi-axes of the axis
, and a direct verification enables one to establish whether the semi-axes of the axis 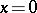 are
are 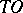 -curves. The behaviour of all trajectories of (1) in a neighbourhood of
-curves. The behaviour of all trajectories of (1) in a neighbourhood of 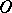 can be determined on the basis of this information as follows.
can be determined on the basis of this information as follows.
If the system (1) has no 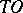 -curves, then
-curves, then 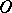 is a centre (cf. Centre of a topological dynamical system), a focus or a centro-focus for it. If the set
is a centre (cf. Centre of a topological dynamical system), a focus or a centro-focus for it. If the set 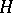 of all
of all 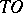 -curves of (1) is non-empty, then the information about its asymptotic behaviour at
-curves of (1) is non-empty, then the information about its asymptotic behaviour at 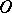 obtained by the Frommer method enables one to split
obtained by the Frommer method enables one to split  into a finite number of non-intersecting bundles of
into a finite number of non-intersecting bundles of 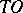 -curves:
-curves: 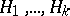 ,
, 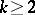 , each of which is either open: it consists of semi-trajectories of one type (positive or negative) that fill a domain, or "closed" : it consists of a single
, each of which is either open: it consists of semi-trajectories of one type (positive or negative) that fill a domain, or "closed" : it consists of a single 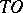 -curve. The representatives
-curve. The representatives 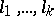 of these bundles have different asymptotic behaviour at
of these bundles have different asymptotic behaviour at 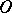 , which enables one to establish a cyclic sequential order for the bundles as one goes round
, which enables one to establish a cyclic sequential order for the bundles as one goes round 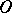 along a circle
along a circle 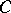 of small radius
of small radius  , and they divide the disc bounded by
, and they divide the disc bounded by 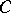 into
into 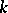 sectors
sectors  .
.
Suppose that the sector 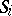 ,
, 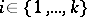 , has as its lateral edges the
, has as its lateral edges the 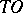 -curves
-curves 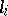 and
and 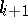 , where
, where 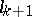 is the same as
is the same as 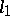 . Then
. Then 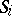 is: a) elliptic, b) hyperbolic or c) parabolic, according to whether the bundles
is: a) elliptic, b) hyperbolic or c) parabolic, according to whether the bundles 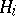 and
and 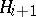 are respectively a) both open, b) both "closed" or c) of different types.
are respectively a) both open, b) both "closed" or c) of different types.
Thus, the Frommer method enables one, in a finite number of steps, either to find, for the system (1), a cyclic sequence of hyperbolic, parabolic and elliptic sectors joined to the point 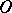 , and thereby completely to determine the topological type of the distribution of its trajectories in a neighbourhood of
, and thereby completely to determine the topological type of the distribution of its trajectories in a neighbourhood of  , or to show that the problem of distinguishing between centre, focus and centro-focus arises at
, or to show that the problem of distinguishing between centre, focus and centro-focus arises at 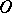 (cf. Centre and focus problem).
(cf. Centre and focus problem).
An account of the method was given by M. Frommer [1]. It can also be adapted for investigating singular points of third-order systems.
References
| [1] | M. Frommer, "Die Integralkurven einer gewöhnlichen Differentialgleichung erster Ordnung in der Umgebung rationaler Unbestimmtheitsstellen" Math. Ann. , 99 (1928) pp. 222–272 |
| [2] | A.F. Andreev, "Singular points of differential equations" , Minsk (1979) (In Russian) |
Comments
References
| [a1] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) pp. 220–227 |
Frommer method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frommer_method&oldid=14740