Difference between revisions of "Frobenius method"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 110 formulas out of 112 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 112 formulas, 110 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
This method enables one to compute a [[Fundamental system of solutions|fundamental system of solutions]] for a holomorphic differential equation near a regular singular point (cf. also [[Singular point|Singular point]]). | This method enables one to compute a [[Fundamental system of solutions|fundamental system of solutions]] for a holomorphic differential equation near a regular singular point (cf. also [[Singular point|Singular point]]). | ||
Suppose one is given a [[Linear differential operator|linear differential operator]] | Suppose one is given a [[Linear differential operator|linear differential operator]] | ||
| − | + | \begin{equation} \tag{a1} L = \sum _ { n = 0 } ^ { N } a ^ { [ n ] } ( z ) z ^ { n } \left( \frac { d } { d z } \right) ^ { n }, \end{equation} | |
| − | where for | + | where for $n = 0 , \ldots , N$ and some $r > 0$, the functions |
| − | + | \begin{equation} \tag{a2} a ^ { [ n ] } ( z ) = \sum _ { i = 0 } ^ { \infty } a _ { i } ^ { n } z ^ { i } \end{equation} | |
| − | are holomorphic for | + | are holomorphic for $| z | < r$ and $a ^ { N_ 0} \neq 0$ (cf. also [[Analytic function|Analytic function]]). The point $z = 0$ is called a regular singular point of $L$. Formula (a1) gives the differential operator in its Frobenius normal form if $a ^ { [ N ] } ( z ) \equiv 1$. |
The Frobenius method is useful for calculating a fundamental system for the homogeneous linear differential equation | The Frobenius method is useful for calculating a fundamental system for the homogeneous linear differential equation | ||
| − | + | \begin{equation} \tag{a3} L ( u ) = 0 \end{equation} | |
| − | in the domain | + | in the domain $\{ z \in \mathbf{C} : | z | < \epsilon \} \backslash ( - \infty , 0 ]$ near the regular singular point at $z = 0$. Here, $\epsilon > 0$, and for an equation in normal form, actually $\epsilon \geq r$. The cut along some ray is introduced because the solutions $u$ are expected to have an essential singularity at $z = 0$. |
The Frobenius method is a generalization of the treatment of the simpler Euler–Cauchy equation | The Frobenius method is a generalization of the treatment of the simpler Euler–Cauchy equation | ||
| − | + | \begin{equation} \tag{a4} L _ { 0 } ( u ) = 0, \end{equation} | |
| − | where the differential operator | + | where the differential operator $L_0$ is made from (a1) by retaining only the leading terms. The Euler–Cauchy equation can be solved by taking the guess $z = u ^ { \lambda }$ with unknown parameter $\lambda \in \mathbf{C}$. One gets $L _ { 0 } ( u ^ { \lambda } ) = \pi ( \lambda ) z ^ { \lambda }$ with the indicial polynomial |
| − | + | \begin{equation} \tag{a5} \pi ( \lambda ) = \sum _ { n = 0 } ^ { N } ( \lambda + n ) ( \lambda + n - 1 ) \ldots ( \lambda + 1 ) a ^ { n _0} = \end{equation} | |
| − | + | \begin{equation*} = a _ { 0 } ^ { N } \prod _ { i = 1 } ^ { \nu } ( \lambda - \lambda _ { i } ) ^ { n _ { i } }. \end{equation*} | |
| − | In the following, the zeros | + | In the following, the zeros $\lambda _ { i }$ of the indicial polynomial will be ordered by requiring |
| − | + | \begin{equation*} \operatorname { Re } \lambda _ { 1 } \geq \ldots \geq \operatorname { Re } \lambda _ { \nu }. \end{equation*} | |
| − | It is assumed that all | + | It is assumed that all $\nu$ roots are different and one denotes their multiplicities by $n_i$. |
The method of Frobenius starts with the guess | The method of Frobenius starts with the guess | ||
| − | + | \begin{equation} \tag{a6} u ( z , \lambda ) = z ^ { \lambda } \sum _ { k = 0 } ^ { \infty } c _ { k } ( \lambda ) z ^ { k }, \end{equation} | |
| − | with an undetermined parameter | + | with an undetermined parameter $\lambda \in \mathbf{C}$. The coefficients <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120210/f12021030.png"/> have to be calculated by requiring that |
| − | + | \begin{equation} \tag{a7} L ( u ( z , \lambda ) ) = \pi ( \lambda ) z ^ { \lambda }. \end{equation} | |
| − | This requirement leads to | + | This requirement leads to $c _ { 0 } \equiv 1$ and |
| − | + | \begin{equation} \tag{a8} c _ { j } ( \lambda ) = - \sum _ { k = 0 } ^ { j - 1 } \frac { c _ { k } ( \lambda ) p _ { j - k } ( \lambda + k ) } { \pi ( \lambda + j ) } \end{equation} | |
| − | as a recursion formula for | + | as a recursion formula for $c_{j}$ for all $j \geq 1$. Here, $p _ { j } ( \lambda )$ are polynomials in $\lambda$ of degree at most $N$, which are given below. |
| − | The easy generic case occurs if the indicial polynomial has only simple zeros and their differences | + | The easy generic case occurs if the indicial polynomial has only simple zeros and their differences $\lambda _ { i } - \lambda _ { j }$ are never integer valued. Under these assumptions, the $N$ functions |
| − | + | \begin{equation*} u ( z , \lambda _ { 1 } ) = z ^ { \lambda _ { 1 } } + \ldots , \ldots , u ( z , \lambda _ { N } ) = z ^ { \lambda _ { N } } +\dots \end{equation*} | |
are a fundamental system of solutions of (a3). | are a fundamental system of solutions of (a3). | ||
==Complications.== | ==Complications.== | ||
| − | Complications can arise if the generic assumption made above is not satisfied. Putting | + | Complications can arise if the generic assumption made above is not satisfied. Putting $\lambda = \lambda _ { i }$ in (a6), obtaining solutions of (a3) can be impossible because of poles of the coefficients $c_j ( \lambda )$. These solutions are rational functions of $\lambda$ with possible poles at the poles of $c _ { 1 } ( \lambda ) , \ldots , c _ { j - 1} ( \lambda )$ as well as at $\lambda _ { 1 } + j , \ldots , \lambda _ { \nu } + j$. |
| − | The poles are compensated for by multiplying | + | The poles are compensated for by multiplying $u ( z , \lambda )$ at first with powers of $\lambda - \lambda _ { i }$ and differentiation by the parameter $\lambda$ before setting $\lambda = \lambda _ { i }$. |
| − | Since the general situation is rather complex, two special cases are given first. Let | + | Since the general situation is rather complex, two special cases are given first. Let $\mathbf{N}$ denote the set of natural numbers starting at $1$ (i.e., excluding $0$). Note that neither of the special cases below does exclude the simple generic case above. |
All solutions have expansions of the form | All solutions have expansions of the form | ||
| − | + | \begin{equation*} u _ { i l } = z ^ { \lambda _ { i } } \sum _ { j = 0 } ^ { l } \sum _ { k = 0 } ^ { \infty } b _ { j k } ( \operatorname { log } z ) ^ { j } z ^ { k }. \end{equation*} | |
| − | The leading term | + | The leading term $b _ { l0 } ( \operatorname { log } z ) ^ { l } z ^ { \lambda _ { i } }$ is useful as a marker for the different solutions. Because for $i = 1 , \dots , \nu$ and $l = 0 , \dots , n _ { i } - 1$, all leading terms are different, the method of Frobenius does indeed yield a fundamental system of $N$ linearly independent solutions of the differential equation (a3). |
===Special case 1.=== | ===Special case 1.=== | ||
| − | For any | + | For any $i = 1 , \dots , \nu$, the zero $\lambda _ { i }$ of the indicial polynomial has multiplicity $n _ { i } \geq 1$, but none of the numbers $\lambda _ { 1 } - \lambda _ { i } , \ldots , \lambda _ { i - 1 } - \lambda _ { i }$ is a natural number. |
In this case, the functions | In this case, the functions | ||
| − | + | \begin{equation*} u ( z , \lambda _ { i } ) = z ^ { \lambda _ { i } } + \ldots , \end{equation*} | |
| − | + | \begin{equation*} \frac { \partial } { \partial \lambda } u ( z , \lambda _ { i } ) = ( \operatorname { log } z ) z ^ { \lambda_i } +\dots \dots \end{equation*} | |
| − | + | \begin{equation*} \left( \frac { \partial } { \partial \lambda } \right) ^ { ( n _ { i } - 1 ) } u ( z , \lambda _ { i } ) = ( \operatorname { log } z ) ^ { n _ { i } - 1 } z ^ { \lambda _ { i } } +\dots \end{equation*} | |
| − | are | + | are $n_i$ linearly independent solutions of the differential equation (a3). |
===Special case 2.=== | ===Special case 2.=== | ||
| − | Suppose | + | Suppose $\lambda _ { 1 } - \lambda _ { 2 } \in \mathbf{N}$. |
Then the functions | Then the functions | ||
| − | + | \begin{equation*} ( \frac { \partial } { \partial \lambda } ) ^ { n _ { 1 } + l } [ u ( z , \lambda ) ( \lambda - \lambda _ { 2 } ) ^ { n _ { 1 } } ] = \end{equation*} | |
| − | + | \begin{equation*} = \frac { ( n _ { 1 } + l ) ! } { l ! } ( \operatorname { log } z ) ^ { l } z ^ { \lambda _ { 2 } } + \ldots, \end{equation*} | |
| − | all with | + | all with $\lambda = \lambda _ { 2 }$ and $l = 0 , \dots , n _ { 2 } - 1$, are $n_{2}$ linearly independent solutions of the differential equation (a3). The solution for $l = 0$ may contain logarithmic terms in the higher powers, starting with $( \operatorname { log } z ) z ^ { \lambda _ { 1 } }$. |
===Special case 3.=== | ===Special case 3.=== | ||
| − | Let | + | Let $1 \leq j \leq \nu$ and let $\lambda _ { i }$ be a zero of the indicial polynomial of multiplicity $n_i$ for $i = 1 , \dots , j - 1$. |
| − | In this case, define | + | In this case, define $m_j$ to be the sum of those multiplicities for which $\lambda _ { i } - \lambda _ { j } \in \mathbf{N}$. Hence, |
| − | + | \begin{equation*} m _ { j } = \sum \{ n _ { i } : 1 \leq i < j \ \text{ and } \ \lambda _ { i } - \lambda _ { j } \in \mathbf{N} \}. \end{equation*} | |
The functions | The functions | ||
| − | + | \begin{equation*} ( \frac { \partial } { \partial \lambda } ) ^ { m _ { j } + l } \left[ u ( z , \lambda ) ( \lambda - \lambda _ { j } ) ^ { m _ { j } } \right] = \end{equation*} | |
| − | + | \begin{equation*} = \frac { ( m _ { j } + l ) ! } { l ! } ( \operatorname { log } z ) ^ { l } z ^ { \lambda _ { j } } + \ldots, \end{equation*} | |
| − | with | + | with $l = 0 , \dots , n _ { j } - 1$ and $\lambda = \lambda _ { j }$, are $n_j$ linearly independent solutions of the differential equation (a3). |
The method looks simpler in the most common case of a differential operator | The method looks simpler in the most common case of a differential operator | ||
| − | + | \begin{equation} \tag{a9} L = a ^ { [ 2 ] } ( z ) z ^ { 2 } \left( \frac { d } { d z } \right) ^ { 2 } + a ^ { [ 1 ] } ( z ) z \left( \frac { d } { d z } \right) + a ^ { [ 0 ] } ( z ). \end{equation} | |
| − | Here, one has to to assume that | + | Here, one has to to assume that $a ^ { 2_0 } \neq 0$ to obtain a regular singular point. The indicial polynomial is simply |
| − | + | \begin{equation*} \pi ( \lambda ) = ( \lambda + 2 ) ( \lambda + 1 ) a ^ { 2_0 } + ( \lambda + 1 ) a ^ { 1_0 } + a ^ { 0_0 } = \end{equation*} | |
| − | + | \begin{equation*} = a ^ { 2 } o ( \lambda - \lambda _ { 1 } ) ( \lambda - \lambda _ { 2 } ). \end{equation*} | |
Only two special cases can occur: | Only two special cases can occur: | ||
| − | 1) | + | 1) $\lambda _ { 1 } = \lambda _ { 2 }$. The functions |
| − | + | \begin{equation*} u ( z , \lambda _ { 1 } ) = z ^ { \lambda _ { 1 } } + \ldots, \end{equation*} | |
| − | + | \begin{equation*} \frac { \partial u } { \partial \lambda } ( z , \lambda _ { 1 } ) = ( \operatorname { log } z ) z ^ { \lambda _ { 1 } } \end{equation*} | |
are a fundamental system. | are a fundamental system. | ||
| − | 2) | + | 2) $\lambda _ { 1 } - \lambda _ { 2 } \in \mathbf{N}$. The functions |
| − | + | \begin{equation*} u ( z , \lambda _ { 1 } ) = z ^ { \lambda _ { 1 } } + \ldots, \end{equation*} | |
| − | + | \begin{equation*} ( \frac { \partial } { \partial \lambda } ) [ u ( z , \lambda ) ( \lambda - \lambda _ { 2 } ) ] = z ^ { \lambda_2 } + \ldots , \end{equation*} | |
| − | with | + | with $\lambda = \lambda _ { 2 }$ in the second function, are two linearly independent solutions of the differential equation (a9). The second solution can contain logarithmic terms in the higher powers starting with $( \operatorname { log } z ) z ^ { \lambda _ { 1 } }$. |
The Frobenius method has been used very successfully to develop a theory of analytic differential equations, especially for the equations of Fuchsian type, where all singular points assumed to be regular (cf. also [[Fuchsian equation|Fuchsian equation]]). A similar method of solution can be used for matrix equations of the first order, too. An adaption of the Frobenius method to non-linear problems is restricted to exceptional cases. The approach does produce special separatrix-type solutions for the Emden–Fowler equation, where the non-linear term contains only powers. | The Frobenius method has been used very successfully to develop a theory of analytic differential equations, especially for the equations of Fuchsian type, where all singular points assumed to be regular (cf. also [[Fuchsian equation|Fuchsian equation]]). A similar method of solution can be used for matrix equations of the first order, too. An adaption of the Frobenius method to non-linear problems is restricted to exceptional cases. The approach does produce special separatrix-type solutions for the Emden–Fowler equation, where the non-linear term contains only powers. | ||
| − | ==Computation of the polynomials | + | ==Computation of the polynomials $p _ { j } ( \lambda )$.== |
In the guess | In the guess | ||
| − | + | \begin{equation*} u ( z , \lambda ) = z ^ { \lambda } \sum _ { k = 0 } ^ { \infty } c _ { k } ( \lambda ) z ^ { k }, \end{equation*} | |
| − | the coefficients <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120210/f120210101.png" /> have to be calculated from the requirement (a7). Indeed (a1) and (a2) imply | + | the coefficients <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120210/f120210101.png"/> have to be calculated from the requirement (a7). Indeed (a1) and (a2) imply |
| − | + | \begin{equation*} L ( u ( z , \lambda ) ) = \end{equation*} | |
| − | + | \begin{equation*} = [ \sum _ { i = 0 } ^ { \infty } \sum _ { n = 0 } ^ { N } a _ { i } ^ { n } z ^ { n + i } ( \frac { \partial } { \partial z } ) ^ { n } ] [ \sum _ { k = 0 } ^ { \infty } c _ { k } ( \lambda ) z ^ { \lambda + k } ] = \end{equation*} | |
| − | + | \begin{equation*} = \sum _ { i = 0 } ^ { \infty } \sum _ { k = 0 } ^ { \infty } c _ { k } ( \lambda ) z ^ { i } \sum _ { n = 0 } ^ { N } a _ { i } ^ { n } z ^ { n } \left( \frac { \partial } { \partial z } \right) ^ { n } z ^ { \lambda + k } = \end{equation*} | |
| − | + | \begin{equation*} = \sum _ { i = 0 } ^ { \infty } \sum _ { k = 0 } ^ { \infty } c _ { k } ( \lambda ) z ^ { i } p _ { i } ( \lambda + k ) z ^ { \lambda + k } = \end{equation*} | |
| − | + | \begin{equation*} = z ^ { \lambda } \sum _ { j = 0 } ^ { \infty } z ^ { j } \left[ \sum _ { i + k = j } c _ { k } ( \lambda ) p _ { i } ( \lambda + k ) \right] = \end{equation*} | |
| − | + | \begin{equation*} = c _ { 0 } z ^ { \lambda } \pi ( \lambda ) + \end{equation*} | |
| − | + | \begin{equation*} + z ^ { \lambda } \sum _ { j = 1 } ^ { \infty } z ^ { j } \left[ c _ { j } ( \lambda ) \pi ( \lambda + j ) + \sum _ { k = 0 } ^ { j - 1 } c _ { k } ( \lambda ) p _ { j - k } ( \lambda + k ) \right]. \end{equation*} | |
| − | Here, | + | Here, $p _ { i } ( \lambda )$ are polynomials of degree at most $N$ determined by setting |
| − | + | \begin{equation*} p _ { i } ( z ) z ^ { \lambda } = \sum _ { n = 0 } ^ { N } a ^ { n _ { i } } z ^ { n } ( \frac { \partial } { \partial z } ) ^ { n } z ^ { \lambda }. \end{equation*} | |
| − | Because of (a7), one finds | + | Because of (a7), one finds $c _ { 0 } \equiv 1$ and the recursion formula (a8). |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> R. Redheffer, "Differential equations, theory and applications" , Jones and Bartlett (1991)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> F. Rothe, "A variant of Frobenius' method for the Emden–Fowler equation" ''Applicable Anal.'' , '''66''' (1997) pp. 217–245</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> D. Zwillinger, "Handbook of differential equations" , Acad. Press (1989)</td></tr></table> |
Revision as of 16:58, 1 July 2020
This method enables one to compute a fundamental system of solutions for a holomorphic differential equation near a regular singular point (cf. also Singular point).
Suppose one is given a linear differential operator
\begin{equation} \tag{a1} L = \sum _ { n = 0 } ^ { N } a ^ { [ n ] } ( z ) z ^ { n } \left( \frac { d } { d z } \right) ^ { n }, \end{equation}
where for $n = 0 , \ldots , N$ and some $r > 0$, the functions
\begin{equation} \tag{a2} a ^ { [ n ] } ( z ) = \sum _ { i = 0 } ^ { \infty } a _ { i } ^ { n } z ^ { i } \end{equation}
are holomorphic for $| z | < r$ and $a ^ { N_ 0} \neq 0$ (cf. also Analytic function). The point $z = 0$ is called a regular singular point of $L$. Formula (a1) gives the differential operator in its Frobenius normal form if $a ^ { [ N ] } ( z ) \equiv 1$.
The Frobenius method is useful for calculating a fundamental system for the homogeneous linear differential equation
\begin{equation} \tag{a3} L ( u ) = 0 \end{equation}
in the domain $\{ z \in \mathbf{C} : | z | < \epsilon \} \backslash ( - \infty , 0 ]$ near the regular singular point at $z = 0$. Here, $\epsilon > 0$, and for an equation in normal form, actually $\epsilon \geq r$. The cut along some ray is introduced because the solutions $u$ are expected to have an essential singularity at $z = 0$.
The Frobenius method is a generalization of the treatment of the simpler Euler–Cauchy equation
\begin{equation} \tag{a4} L _ { 0 } ( u ) = 0, \end{equation}
where the differential operator $L_0$ is made from (a1) by retaining only the leading terms. The Euler–Cauchy equation can be solved by taking the guess $z = u ^ { \lambda }$ with unknown parameter $\lambda \in \mathbf{C}$. One gets $L _ { 0 } ( u ^ { \lambda } ) = \pi ( \lambda ) z ^ { \lambda }$ with the indicial polynomial
\begin{equation} \tag{a5} \pi ( \lambda ) = \sum _ { n = 0 } ^ { N } ( \lambda + n ) ( \lambda + n - 1 ) \ldots ( \lambda + 1 ) a ^ { n _0} = \end{equation}
\begin{equation*} = a _ { 0 } ^ { N } \prod _ { i = 1 } ^ { \nu } ( \lambda - \lambda _ { i } ) ^ { n _ { i } }. \end{equation*}
In the following, the zeros $\lambda _ { i }$ of the indicial polynomial will be ordered by requiring
\begin{equation*} \operatorname { Re } \lambda _ { 1 } \geq \ldots \geq \operatorname { Re } \lambda _ { \nu }. \end{equation*}
It is assumed that all $\nu$ roots are different and one denotes their multiplicities by $n_i$.
The method of Frobenius starts with the guess
\begin{equation} \tag{a6} u ( z , \lambda ) = z ^ { \lambda } \sum _ { k = 0 } ^ { \infty } c _ { k } ( \lambda ) z ^ { k }, \end{equation}
with an undetermined parameter $\lambda \in \mathbf{C}$. The coefficients 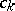 have to be calculated by requiring that
have to be calculated by requiring that
\begin{equation} \tag{a7} L ( u ( z , \lambda ) ) = \pi ( \lambda ) z ^ { \lambda }. \end{equation}
This requirement leads to $c _ { 0 } \equiv 1$ and
\begin{equation} \tag{a8} c _ { j } ( \lambda ) = - \sum _ { k = 0 } ^ { j - 1 } \frac { c _ { k } ( \lambda ) p _ { j - k } ( \lambda + k ) } { \pi ( \lambda + j ) } \end{equation}
as a recursion formula for $c_{j}$ for all $j \geq 1$. Here, $p _ { j } ( \lambda )$ are polynomials in $\lambda$ of degree at most $N$, which are given below.
The easy generic case occurs if the indicial polynomial has only simple zeros and their differences $\lambda _ { i } - \lambda _ { j }$ are never integer valued. Under these assumptions, the $N$ functions
\begin{equation*} u ( z , \lambda _ { 1 } ) = z ^ { \lambda _ { 1 } } + \ldots , \ldots , u ( z , \lambda _ { N } ) = z ^ { \lambda _ { N } } +\dots \end{equation*}
are a fundamental system of solutions of (a3).
Complications.
Complications can arise if the generic assumption made above is not satisfied. Putting $\lambda = \lambda _ { i }$ in (a6), obtaining solutions of (a3) can be impossible because of poles of the coefficients $c_j ( \lambda )$. These solutions are rational functions of $\lambda$ with possible poles at the poles of $c _ { 1 } ( \lambda ) , \ldots , c _ { j - 1} ( \lambda )$ as well as at $\lambda _ { 1 } + j , \ldots , \lambda _ { \nu } + j$.
The poles are compensated for by multiplying $u ( z , \lambda )$ at first with powers of $\lambda - \lambda _ { i }$ and differentiation by the parameter $\lambda$ before setting $\lambda = \lambda _ { i }$.
Since the general situation is rather complex, two special cases are given first. Let $\mathbf{N}$ denote the set of natural numbers starting at $1$ (i.e., excluding $0$). Note that neither of the special cases below does exclude the simple generic case above.
All solutions have expansions of the form
\begin{equation*} u _ { i l } = z ^ { \lambda _ { i } } \sum _ { j = 0 } ^ { l } \sum _ { k = 0 } ^ { \infty } b _ { j k } ( \operatorname { log } z ) ^ { j } z ^ { k }. \end{equation*}
The leading term $b _ { l0 } ( \operatorname { log } z ) ^ { l } z ^ { \lambda _ { i } }$ is useful as a marker for the different solutions. Because for $i = 1 , \dots , \nu$ and $l = 0 , \dots , n _ { i } - 1$, all leading terms are different, the method of Frobenius does indeed yield a fundamental system of $N$ linearly independent solutions of the differential equation (a3).
Special case 1.
For any $i = 1 , \dots , \nu$, the zero $\lambda _ { i }$ of the indicial polynomial has multiplicity $n _ { i } \geq 1$, but none of the numbers $\lambda _ { 1 } - \lambda _ { i } , \ldots , \lambda _ { i - 1 } - \lambda _ { i }$ is a natural number.
In this case, the functions
\begin{equation*} u ( z , \lambda _ { i } ) = z ^ { \lambda _ { i } } + \ldots , \end{equation*}
\begin{equation*} \frac { \partial } { \partial \lambda } u ( z , \lambda _ { i } ) = ( \operatorname { log } z ) z ^ { \lambda_i } +\dots \dots \end{equation*}
\begin{equation*} \left( \frac { \partial } { \partial \lambda } \right) ^ { ( n _ { i } - 1 ) } u ( z , \lambda _ { i } ) = ( \operatorname { log } z ) ^ { n _ { i } - 1 } z ^ { \lambda _ { i } } +\dots \end{equation*}
are $n_i$ linearly independent solutions of the differential equation (a3).
Special case 2.
Suppose $\lambda _ { 1 } - \lambda _ { 2 } \in \mathbf{N}$.
Then the functions
\begin{equation*} ( \frac { \partial } { \partial \lambda } ) ^ { n _ { 1 } + l } [ u ( z , \lambda ) ( \lambda - \lambda _ { 2 } ) ^ { n _ { 1 } } ] = \end{equation*}
\begin{equation*} = \frac { ( n _ { 1 } + l ) ! } { l ! } ( \operatorname { log } z ) ^ { l } z ^ { \lambda _ { 2 } } + \ldots, \end{equation*}
all with $\lambda = \lambda _ { 2 }$ and $l = 0 , \dots , n _ { 2 } - 1$, are $n_{2}$ linearly independent solutions of the differential equation (a3). The solution for $l = 0$ may contain logarithmic terms in the higher powers, starting with $( \operatorname { log } z ) z ^ { \lambda _ { 1 } }$.
Special case 3.
Let $1 \leq j \leq \nu$ and let $\lambda _ { i }$ be a zero of the indicial polynomial of multiplicity $n_i$ for $i = 1 , \dots , j - 1$.
In this case, define $m_j$ to be the sum of those multiplicities for which $\lambda _ { i } - \lambda _ { j } \in \mathbf{N}$. Hence,
\begin{equation*} m _ { j } = \sum \{ n _ { i } : 1 \leq i < j \ \text{ and } \ \lambda _ { i } - \lambda _ { j } \in \mathbf{N} \}. \end{equation*}
The functions
\begin{equation*} ( \frac { \partial } { \partial \lambda } ) ^ { m _ { j } + l } \left[ u ( z , \lambda ) ( \lambda - \lambda _ { j } ) ^ { m _ { j } } \right] = \end{equation*}
\begin{equation*} = \frac { ( m _ { j } + l ) ! } { l ! } ( \operatorname { log } z ) ^ { l } z ^ { \lambda _ { j } } + \ldots, \end{equation*}
with $l = 0 , \dots , n _ { j } - 1$ and $\lambda = \lambda _ { j }$, are $n_j$ linearly independent solutions of the differential equation (a3).
The method looks simpler in the most common case of a differential operator
\begin{equation} \tag{a9} L = a ^ { [ 2 ] } ( z ) z ^ { 2 } \left( \frac { d } { d z } \right) ^ { 2 } + a ^ { [ 1 ] } ( z ) z \left( \frac { d } { d z } \right) + a ^ { [ 0 ] } ( z ). \end{equation}
Here, one has to to assume that $a ^ { 2_0 } \neq 0$ to obtain a regular singular point. The indicial polynomial is simply
\begin{equation*} \pi ( \lambda ) = ( \lambda + 2 ) ( \lambda + 1 ) a ^ { 2_0 } + ( \lambda + 1 ) a ^ { 1_0 } + a ^ { 0_0 } = \end{equation*}
\begin{equation*} = a ^ { 2 } o ( \lambda - \lambda _ { 1 } ) ( \lambda - \lambda _ { 2 } ). \end{equation*}
Only two special cases can occur:
1) $\lambda _ { 1 } = \lambda _ { 2 }$. The functions
\begin{equation*} u ( z , \lambda _ { 1 } ) = z ^ { \lambda _ { 1 } } + \ldots, \end{equation*}
\begin{equation*} \frac { \partial u } { \partial \lambda } ( z , \lambda _ { 1 } ) = ( \operatorname { log } z ) z ^ { \lambda _ { 1 } } \end{equation*}
are a fundamental system.
2) $\lambda _ { 1 } - \lambda _ { 2 } \in \mathbf{N}$. The functions
\begin{equation*} u ( z , \lambda _ { 1 } ) = z ^ { \lambda _ { 1 } } + \ldots, \end{equation*}
\begin{equation*} ( \frac { \partial } { \partial \lambda } ) [ u ( z , \lambda ) ( \lambda - \lambda _ { 2 } ) ] = z ^ { \lambda_2 } + \ldots , \end{equation*}
with $\lambda = \lambda _ { 2 }$ in the second function, are two linearly independent solutions of the differential equation (a9). The second solution can contain logarithmic terms in the higher powers starting with $( \operatorname { log } z ) z ^ { \lambda _ { 1 } }$.
The Frobenius method has been used very successfully to develop a theory of analytic differential equations, especially for the equations of Fuchsian type, where all singular points assumed to be regular (cf. also Fuchsian equation). A similar method of solution can be used for matrix equations of the first order, too. An adaption of the Frobenius method to non-linear problems is restricted to exceptional cases. The approach does produce special separatrix-type solutions for the Emden–Fowler equation, where the non-linear term contains only powers.
Computation of the polynomials $p _ { j } ( \lambda )$.
In the guess
\begin{equation*} u ( z , \lambda ) = z ^ { \lambda } \sum _ { k = 0 } ^ { \infty } c _ { k } ( \lambda ) z ^ { k }, \end{equation*}
the coefficients 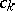 have to be calculated from the requirement (a7). Indeed (a1) and (a2) imply
have to be calculated from the requirement (a7). Indeed (a1) and (a2) imply
\begin{equation*} L ( u ( z , \lambda ) ) = \end{equation*}
\begin{equation*} = [ \sum _ { i = 0 } ^ { \infty } \sum _ { n = 0 } ^ { N } a _ { i } ^ { n } z ^ { n + i } ( \frac { \partial } { \partial z } ) ^ { n } ] [ \sum _ { k = 0 } ^ { \infty } c _ { k } ( \lambda ) z ^ { \lambda + k } ] = \end{equation*}
\begin{equation*} = \sum _ { i = 0 } ^ { \infty } \sum _ { k = 0 } ^ { \infty } c _ { k } ( \lambda ) z ^ { i } \sum _ { n = 0 } ^ { N } a _ { i } ^ { n } z ^ { n } \left( \frac { \partial } { \partial z } \right) ^ { n } z ^ { \lambda + k } = \end{equation*}
\begin{equation*} = \sum _ { i = 0 } ^ { \infty } \sum _ { k = 0 } ^ { \infty } c _ { k } ( \lambda ) z ^ { i } p _ { i } ( \lambda + k ) z ^ { \lambda + k } = \end{equation*}
\begin{equation*} = z ^ { \lambda } \sum _ { j = 0 } ^ { \infty } z ^ { j } \left[ \sum _ { i + k = j } c _ { k } ( \lambda ) p _ { i } ( \lambda + k ) \right] = \end{equation*}
\begin{equation*} = c _ { 0 } z ^ { \lambda } \pi ( \lambda ) + \end{equation*}
\begin{equation*} + z ^ { \lambda } \sum _ { j = 1 } ^ { \infty } z ^ { j } \left[ c _ { j } ( \lambda ) \pi ( \lambda + j ) + \sum _ { k = 0 } ^ { j - 1 } c _ { k } ( \lambda ) p _ { j - k } ( \lambda + k ) \right]. \end{equation*}
Here, $p _ { i } ( \lambda )$ are polynomials of degree at most $N$ determined by setting
\begin{equation*} p _ { i } ( z ) z ^ { \lambda } = \sum _ { n = 0 } ^ { N } a ^ { n _ { i } } z ^ { n } ( \frac { \partial } { \partial z } ) ^ { n } z ^ { \lambda }. \end{equation*}
Because of (a7), one finds $c _ { 0 } \equiv 1$ and the recursion formula (a8).
References
| [a1] | R. Redheffer, "Differential equations, theory and applications" , Jones and Bartlett (1991) |
| [a2] | F. Rothe, "A variant of Frobenius' method for the Emden–Fowler equation" Applicable Anal. , 66 (1997) pp. 217–245 |
| [a3] | D. Zwillinger, "Handbook of differential equations" , Acad. Press (1989) |
Frobenius method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frobenius_method&oldid=12220