Frobenius formula
A formula expressing a relation between the generalized Vandermonde determinant and the ordinary one (see Vandermonde determinant) in terms of sums of powers. The characters of representations of a symmetric group (cf. Representation of the symmetric groups) appear as coefficients in the Frobenius formula.
Let  be independent variables. For any
be independent variables. For any  -tuple
-tuple 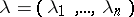 of non-negative integers satisfying the condition
of non-negative integers satisfying the condition 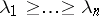 , let
, let
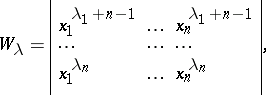 |
so that 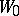 is the ordinary Vandermonde determinant. Let
is the ordinary Vandermonde determinant. Let 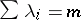 ; then after discarding zeros the
; then after discarding zeros the  -tuple
-tuple 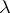 can be regarded as a partition of the number
can be regarded as a partition of the number 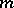 . Consider the corresponding irreducible representation
. Consider the corresponding irreducible representation 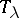 of the symmetric group
of the symmetric group 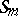 . For any partition
. For any partition 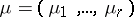 of
of 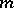 one denotes by
one denotes by 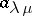 the value of the character of
the value of the character of 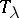 on the conjugacy class of
on the conjugacy class of 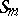 determined by
determined by 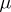 , and by
, and by 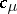 the order of the centralizer of any permutation in this class. Let
the order of the centralizer of any permutation in this class. Let 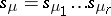 , where
, where 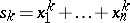 . Then
. Then
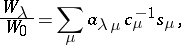 |
where the sum is taken over all (unordered) partitions of 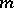 . Here, if the partition
. Here, if the partition 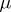 contains
contains 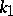 ones,
ones, 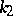 twos, etc., then
twos, etc., then
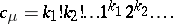 |
If  , then Frobenius' formula can be put in the form
, then Frobenius' formula can be put in the form
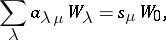 |
where the sum is taken over all partitions of 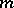 (adding the appropriate number of zeros). The last formula can be used to compute the characters of the symmetric group. Namely,
(adding the appropriate number of zeros). The last formula can be used to compute the characters of the symmetric group. Namely, 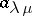 is the coefficient of
is the coefficient of 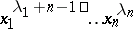 in the polynomial
in the polynomial 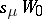 .
.
References
| [1] | F.D. Murnagan, "The theory of group representations" , Johns Hopkins Univ. Press (1938) |
Comments
See also Character of a representation of a group.
References
| [a1] | H. Boerner, "Representations of groups" , North-Holland (1970) (Translated from German) |
| [a2] | D.E. Littlewood, "The theory of group characters and matrix representations of groups" , Clarendon Press (1950) |
| [a3] | I.G. Macdonald, "Symmetric functions and Hall polynomials" , Clarendon Press (1979) |
| [a4] | B.G. Wybourne, "Symmetry principles and atomic spectroscopy" , Wiley (Interscience) (1970) |
Frobenius formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frobenius_formula&oldid=15262