Frobenius automorphism

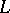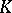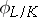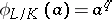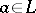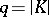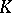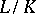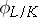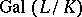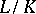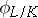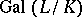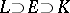An element of a Galois group of a special type. It plays a fundamental role in class field theory. Suppose that is an algebraic extension of a finite field . Then the Frobenius automorphism is the automorphism defined by the formula for all , where (the cardinality of ). If is a finite extension, then generates the Galois group . For an infinite extension , is a topological generator of . If and 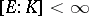, then .

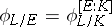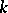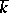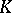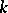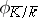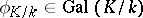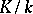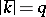Suppose that is a local field with a finite residue field , and that is an unramified extension of . Then the Frobenius automorphism of the extension of residue fields can be uniquely lifted to an automorphism , called the Frobenius automorphism of the unramified extension . Let , let 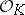be the ring of integers of 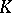, and let 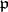be a maximal ideal in 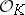. Then the Frobenius automorphism 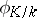is uniquely determined by the condition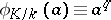 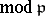for every 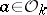. If 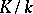is an arbitrary Galois extension of local fields, then sometimes any automorphism 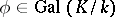that induces a Frobenius automorphism in the sense indicated above on the maximal unramified subextension of 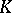is called a Frobenius automorphism of .

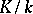Let 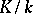be a Galois extension of global fields, let 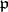be a prime ideal of 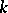, and let 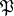be some prime ideal of 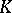over 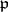. Suppose also that 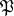is unramified in 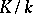and that 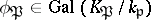is the Frobenius automorphism of the unramified extension of local fields 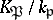. If one identifies the Galois group 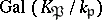with the decomposition subgroup of 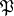in 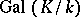, one can regard 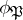as an element of 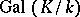. This element is called the Frobenius automorphism corresponding to the prime ideal 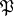. If 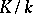is a finite extension, then, according to the Chebotarev density theorem, for any automorphism 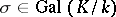there is an infinite number of prime ideals 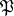, unramified in 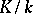, such that 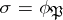. For an Abelian extension 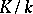, the element 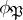depends only on 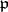. In this case 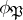is denoted by 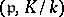and is called the Artin symbol of the prime ideal .

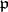References

[1]	A. Weil, "Basic number theory" , Springer (1974)