Frobenius algebra

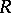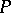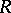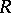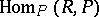A finite-dimensional algebra over a field such that the left -modules and are isomorphic. In the language of representations this means that the left and right regular representations are equivalent. Every group algebra of a finite group over a field is a Frobenius algebra. Every Frobenius algebra is a quasi-Frobenius ring. The converse is not true. The following properties of a finite-dimensional 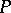-algebra 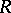are equivalent:

1) 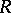is a Frobenius algebra;

2) there is a non-degenerate bilinear form 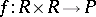such that 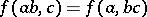for all ;

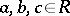3) if 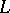is a left and 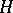is a right ideal of 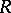, then (see Annihilator)

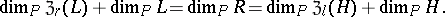Frobenius algebras essentially first appeared in the papers of G. Frobenius [3].

References

[1]	C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)
[2]	C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1973–1976)
[3]	G. Frobenius, "Theorie der hyperkomplexen Grössen" Sitzungsber. Königl. Preuss. Akad. Wiss. : 24 (1903) pp. 504–537; 634–645

Comments

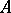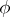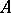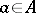A criterion for an algebra to be Frobenius is that there is a linear form on such that if for all then 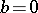. If, moreover, 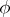satisfies 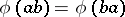for all 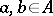, then 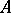is called a symmetric algebra.

Examples of symmetric algebras are semi-simple algebras and group algebras.