Free resolution
From Encyclopedia of Mathematics
A special case of a projective resolution. Every module 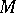 over an associative ring
over an associative ring 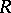 is the quotient module
is the quotient module 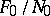 of a free
of a free 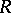 -module
-module 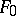 by a submodule
by a submodule 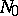 . The submodule
. The submodule 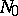 has a similar representation
has a similar representation 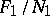 , etc. As a result one obtains an exact sequence of free modules
, etc. As a result one obtains an exact sequence of free modules
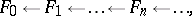 |
called the free resolution of 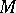 . The canonical homomorphism
. The canonical homomorphism 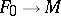 is called a supplementing homomorphism (or augmentation).
is called a supplementing homomorphism (or augmentation).
Comments
See also Free module.
How to Cite This Entry:
Free resolution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_resolution&oldid=12844
Free resolution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_resolution&oldid=12844
This article was adapted from an original article by V.E. Govorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article