Free product
in a class  of universal algebras
of universal algebras 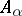 ,
, 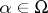 , from
, from 
An algebra 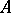 from
from 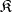 that contains all the
that contains all the  as subalgebras and is such that any family of homomorphisms of the
as subalgebras and is such that any family of homomorphisms of the 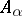 into any other algebra
into any other algebra  from
from 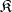 can be uniquely extended to a homomorphism of
can be uniquely extended to a homomorphism of  into
into  . A free product automatically exists if
. A free product automatically exists if 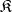 is a variety of universal algebras. Every free algebra is the free product of free algebras generated by a singleton. The free product in the class of Abelian groups coincides with the direct sum. In certain cases there is a description of the subalgebras of a free product, for example, in groups (see Free product of groups), in non-associative algebras, and in Lie algebras.
is a variety of universal algebras. Every free algebra is the free product of free algebras generated by a singleton. The free product in the class of Abelian groups coincides with the direct sum. In certain cases there is a description of the subalgebras of a free product, for example, in groups (see Free product of groups), in non-associative algebras, and in Lie algebras.
A free product in categories of universal algebras coincides with the coproduct in these categories.
Comments
Free products do not always exists in a variety of algebras: for example, the ring of integers modulo  and the ring of integers modulo
and the ring of integers modulo  have no free product in the variety of rings with 1. However, coproducts (which differ from free products in not requiring the canonical homomorphisms
have no free product in the variety of rings with 1. However, coproducts (which differ from free products in not requiring the canonical homomorphisms 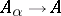 to be injective) always exist in a variety of algebras [a1].
to be injective) always exist in a variety of algebras [a1].
References
| [a1] | F.E.J. Linton, "Coequalizors in categories of algebras" , Seminar on Triples and Categorical Homology Theory , Lect. notes in math. , 80 , Springer (1969) pp. 75–90 |
Free product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_product&oldid=14874