Free magma
From Encyclopedia of Mathematics
Let  be a set. Define sets
be a set. Define sets  ,
,  , inductively as follows:
, inductively as follows:
 |
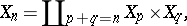 |
where  denotes the disjoint union (see Union of sets). Let
denotes the disjoint union (see Union of sets). Let
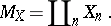 |
There is an obvious binary operation on  : if
: if  ,
, 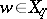 , then the pair
, then the pair 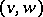 goes to the element
goes to the element  of
of 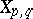 . This is the free magma on
. This is the free magma on  . It has the obvious freeness property: if
. It has the obvious freeness property: if  is any magma and
is any magma and 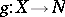 is a function, then there is a unique morphism of magmas
is a function, then there is a unique morphism of magmas  extending
extending  .
.
Certain special subsets of  , called Hall sets (cf. Hall set), are important in combinatorics and the theory of Lie algebras.
, called Hall sets (cf. Hall set), are important in combinatorics and the theory of Lie algebras.
The free magma over 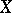 can be identified with the set of binary complete, planar, rooted trees with leaves labelled by
can be identified with the set of binary complete, planar, rooted trees with leaves labelled by  . See Binary tree.
. See Binary tree.
References
| [a1] | N. Bourbaki, "Groupes et algèbres de Lie" , 2: Algèbres de Lie libres , Hermann (1972) |
| [a2] | C. Reutenauer, "Free Lie algebras" , Oxford Univ. Press (1993) |
| [a3] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) |
How to Cite This Entry:
Free magma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_magma&oldid=12862
Free magma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_magma&oldid=12862
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article