Free associative algebra
The algebra 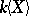 of polynomials over a field
of polynomials over a field  in non-commuting variables in
in non-commuting variables in  . The following universal property determines the algebra
. The following universal property determines the algebra  uniquely up to an isomorphism: There is a mapping
uniquely up to an isomorphism: There is a mapping  such that any mapping from
such that any mapping from  into an associative algebra
into an associative algebra 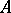 with a unit over
with a unit over  can be factored through
can be factored through  in a unique way. The basic properties of
in a unique way. The basic properties of  are:
are:
1) 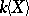 can be imbedded in a skew-field (the Mal'tsev–Neumann theorem);
can be imbedded in a skew-field (the Mal'tsev–Neumann theorem);
2)  has a weak division algorithm, that is, the relation
has a weak division algorithm, that is, the relation
 |
where  , all the
, all the 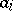 are non-zero
are non-zero 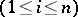 ,
,  , always implies that there are an integer
, always implies that there are an integer  ,
, 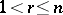 , and elements
, and elements  such that
such that
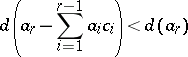 |
and
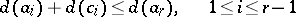 |
(here  is the usual degree of a polynomial
is the usual degree of a polynomial 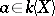 ,
,  );
);
3)  is a left (respectively, right) free ideal ring (that is, any left (respectively, right) ideal of
is a left (respectively, right) free ideal ring (that is, any left (respectively, right) ideal of  is a free module of uniquely determined rank);
is a free module of uniquely determined rank);
4) the centralizer of any non-scalar element of  (that is, the set of elements that commute with a given element) is isomorphic to the algebra of polynomials over
(that is, the set of elements that commute with a given element) is isomorphic to the algebra of polynomials over 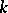 in a single variable (Bergman's theorem).
in a single variable (Bergman's theorem).
References
| [1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [2] | P.M. Cohn, "Free rings and their relations" , Acad. Press (1971) |
'
Free associative algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_associative_algebra&oldid=16680