Difference between revisions of "Fredholm solvability"
m (grammatical structure) |
m (begin latex-ing) |
||
| Line 1: | Line 1: | ||
| − | Let | + | Let $A$ be a real $(n\times n)$-matrix and $b\in R^n$ a vector. |
| − | The Fredholm alternative in | + | The Fredholm alternative in $R^n$ states that the equation $Ax=b$ has a solution if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f1302306.png" /> for every vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f1302307.png" /> satisfying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f1302308.png" />. |
| − | This alternative has many applications, e.g. in bifurcation theory. It can be generalized to abstract spaces. So, let | + | This alternative has many applications, e.g. in bifurcation theory. It can be generalized to abstract spaces. So, let $E$ and $F$ be Banach spaces (cf. [[Banach space|Banach space]]) and let $T:E\rightarrow F$ be a continuous [[Linear operator|linear operator]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023012.png" />, respectively <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023013.png" />, denote the topological dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023014.png" />, respectively <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023015.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023016.png" /> denote the adjoint of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023017.png" /> (cf. also [[Duality|Duality]]; [[Adjoint operator|Adjoint operator]]). Define |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023018.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023018.png" /></td> </tr></table> | ||
| − | An equation | + | An equation $Tx=y$ is said to be normally solvable (in the sense of F. Hausdorff) if it has a solution whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023020.png" /> (cf. also [[Normal solvability|Normal solvability]]). A classical result states that $Tx=y$ is normally solvable if and only if $T(E)$ is closed in $F$. |
In non-linear analysis, this latter result is used as definition of normal solvability for non-linear operators. | In non-linear analysis, this latter result is used as definition of normal solvability for non-linear operators. | ||
Revision as of 18:23, 30 October 2016
Let $A$ be a real $(n\times n)$-matrix and $b\in R^n$ a vector.
The Fredholm alternative in $R^n$ states that the equation $Ax=b$ has a solution if and only if  for every vector
for every vector  satisfying
satisfying  .
.
This alternative has many applications, e.g. in bifurcation theory. It can be generalized to abstract spaces. So, let $E$ and $F$ be Banach spaces (cf. Banach space) and let $T:E\rightarrow F$ be a continuous linear operator. Let 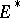 , respectively
, respectively 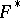 , denote the topological dual of
, denote the topological dual of  , respectively
, respectively 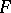 , and let
, and let 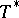 denote the adjoint of
denote the adjoint of 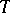 (cf. also Duality; Adjoint operator). Define
(cf. also Duality; Adjoint operator). Define
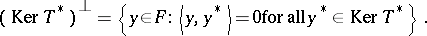 |
An equation $Tx=y$ is said to be normally solvable (in the sense of F. Hausdorff) if it has a solution whenever 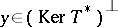 (cf. also Normal solvability). A classical result states that $Tx=y$ is normally solvable if and only if $T(E)$ is closed in $F$.
(cf. also Normal solvability). A classical result states that $Tx=y$ is normally solvable if and only if $T(E)$ is closed in $F$.
In non-linear analysis, this latter result is used as definition of normal solvability for non-linear operators.
The phrase "Fredholm solvability" refers to results and techniques for solving differential and integral equations via the Fredholm alternative and, more generally, the Fredholm-type properties of the operator involved.
References
| [a1] | F. Hausdorff, "Zur Theorie der linearen metrischen Räume" J. Reine Angew. Math. , 167 (1932) pp. 265 Zbl 0003.33104 Zbl 58.1113.05 |
| [a2] | V.A. Kozlov, V.G. Maz'ya, J. Rossmann, "Elliptic boundary value problems in domains with point singularities" , Amer. Math. Soc. (1997) MR1469972 Zbl 0947.35004 |
| [a3] | A.T. Prilepko, D.G. Orlovsky, I.A. Vasin, "Methods for solving inverse problems in mathematical physics" , M. Dekker (2000) MR1748236 Zbl 0947.35173 |
| [a4] | D.G. Orlovskij, "The Fredholm solvability of inverse problems for abstract differential equations" A.N. Tikhonov (ed.) et al. (ed.) , Ill-Posed Problems in the Natural Sciences , VSP (1992) Zbl 0789.35178 |
Fredholm solvability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fredholm_solvability&oldid=39534