Frattini subgroup
Let 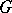 denote an arbitrary group (finite or infinite) and let
denote an arbitrary group (finite or infinite) and let 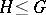 (respectively,
(respectively, 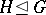 ) mean that
) mean that 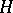 is a subgroup (respectively, a normal subgroup) of
is a subgroup (respectively, a normal subgroup) of 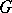 (cf. also Subgroup; Normal subgroup). Let
(cf. also Subgroup; Normal subgroup). Let 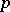 denote a prime number.
denote a prime number.
The intersection of all (proper) maximal subgroups of 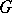 is called the Frattini subgroup of
is called the Frattini subgroup of 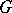 and will be denoted by
and will be denoted by 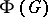 . If
. If 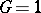 or
or 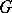 is infinite, then
is infinite, then 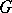 may contain no maximal subgroups, in which case
may contain no maximal subgroups, in which case 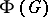 is defined as
is defined as 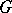 . Clearly,
. Clearly,  is a characteristic (hence normal) subgroup of
is a characteristic (hence normal) subgroup of 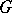 (cf. also Characteristic subgroup).
(cf. also Characteristic subgroup).
The set of non-generators of 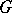 consists of all
consists of all 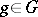 satisfying the following property: If
satisfying the following property: If 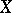 is a non-empty subset of
is a non-empty subset of 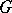 and
and 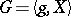 , then
, then 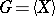 . In 1885, G. Frattini proved [a1] that
. In 1885, G. Frattini proved [a1] that 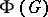 is equal to the set of non-generators of
is equal to the set of non-generators of 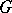 . In particular, if
. In particular, if 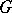 is a finite group and
is a finite group and 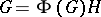 for some subgroup
for some subgroup 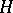 of
of 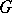 , then
, then 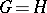 . Using this observation, Frattini proved that the Frattini subgroup of a finite group is nilpotent (cf. also Nilpotent group). This basic result gave
. Using this observation, Frattini proved that the Frattini subgroup of a finite group is nilpotent (cf. also Nilpotent group). This basic result gave 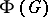 its name. Moreover, his proof was very elegant: if
its name. Moreover, his proof was very elegant: if 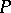 denotes a Sylow
denotes a Sylow 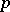 -subgroup (cf. also Sylow subgroup;
-subgroup (cf. also Sylow subgroup; 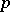 -group) of
-group) of 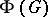 , then he proved that
, then he proved that 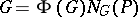 , whence, as remarked above,
, whence, as remarked above, 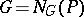 and the nilpotency of
and the nilpotency of 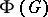 follows. Since then, the enormously useful result that if
follows. Since then, the enormously useful result that if 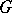 is a finite group,
is a finite group, 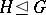 and
and 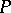 is a Sylow
is a Sylow 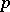 -subgroup of
-subgroup of 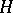 , then
, then 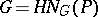 , is usually referred to as the Frattini argument.
, is usually referred to as the Frattini argument.
The Frattini subgroup 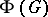 of
of 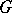 is strongly interrelated with the commutator subgroup
is strongly interrelated with the commutator subgroup  . In 1953, W. Gaschütz proved [a2] that for every (possibly infinite) group
. In 1953, W. Gaschütz proved [a2] that for every (possibly infinite) group  one has
one has 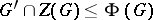 , where
, where 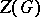 denotes the centre of
denotes the centre of 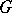 (cf. also Centre of a group). The stronger condition
(cf. also Centre of a group). The stronger condition 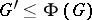 is equivalent to the property that all maximal subgroups of
is equivalent to the property that all maximal subgroups of 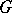 are normal in
are normal in 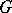 . It follows that if
. It follows that if 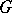 is a nilpotent group, then
is a nilpotent group, then 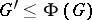 . If
. If 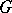 is a finite group, then, as discovered by H. Wielandt,
is a finite group, then, as discovered by H. Wielandt, 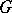 is nilpotent if and only if
is nilpotent if and only if 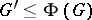 . If
. If 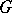 is a finite
is a finite 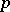 -group, then
-group, then 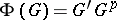 , where
, where 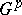 is the subgroup of
is the subgroup of 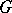 generated by all the
generated by all the 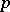 -th powers of elements of
-th powers of elements of 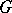 . If
. If 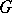 is a finite
is a finite  -group, then
-group, then 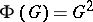 . It follows that if
. It follows that if 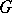 is a finite
is a finite 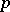 -group, then
-group, then 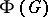 is equal to the intersection of all normal subgroups
is equal to the intersection of all normal subgroups 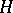 of
of 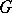 with elementary Abelian quotient groups
with elementary Abelian quotient groups 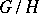 .
.
The Frattini quotient 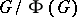 has also some important properties. If
has also some important properties. If 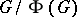 is cyclic (cf. also Cyclic group), then
is cyclic (cf. also Cyclic group), then 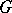 is cyclic. If
is cyclic. If 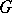 is finite, then
is finite, then 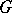 is nilpotent if and only if
is nilpotent if and only if 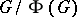 is nilpotent. Moreover, if
is nilpotent. Moreover, if 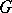 is finite and
is finite and 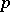 divides
divides 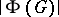 , then
, then 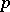 divides also
divides also 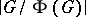 . If
. If 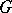 is a finite
is a finite 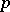 -group, then
-group, then 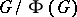 is elementary Abelian and if
is elementary Abelian and if 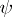 is a
is a 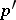 -automorphism of
-automorphism of 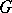 which induces the identity on
which induces the identity on 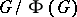 , then, by a theorem of Burnside,
, then, by a theorem of Burnside, 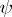 is the identity automorphism of
is the identity automorphism of  .
.
Finally, let 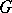 be a group of order
be a group of order 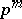 and let
and let 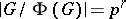 . The Burnside basis theorem states that any minimal generating set of
. The Burnside basis theorem states that any minimal generating set of 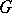 has the same cardinality
has the same cardinality  , and by a theorem of Ph. Hall the order of
, and by a theorem of Ph. Hall the order of 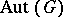 divides
divides 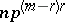 , where
, where 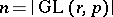 .
.
General references for these and more specific results concerning the Frattini subgroup are [a3], [a4], [a5].
References
| [a1] | G. Frattini, "Intorno alla generazione dei gruppi di operazioni" Rend. Atti Acad. Lincei , 1 : 4 (1885) pp. 281–285; 455–457 |
| [a2] | W. Gaschütz, "Über die 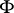 -Untergruppe endlicher Gruppen" Math. Z. , 58 (1953) pp. 160–170 -Untergruppe endlicher Gruppen" Math. Z. , 58 (1953) pp. 160–170 |
| [a3] | B. Huppert, "Endliche Gruppen" , I , Springer (1967) |
| [a4] | D.J.S. Robinson, "A course in the theory of groups" , Springer (1982) |
| [a5] | W.R. Scott, "Group theory" , Prentice-Hall (1964) |
Frattini subgroup. Marcel Herzog (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frattini_subgroup&oldid=14968