Frattini-subgroup(2)
From Encyclopedia of Mathematics
The characteristic subgroup 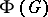 of a group
of a group 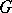 defined as the intersection of all maximal subgroups (cf. Maximal subgroup) of
defined as the intersection of all maximal subgroups (cf. Maximal subgroup) of 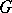 , if there are any; otherwise
, if there are any; otherwise 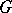 is its own Frattini subgroup. It was introduced by G. Frattini [1]. The Frattini subgroup consists of precisely those elements of
is its own Frattini subgroup. It was introduced by G. Frattini [1]. The Frattini subgroup consists of precisely those elements of 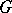 that can be removed from any generating system of the group containing them, that is,
that can be removed from any generating system of the group containing them, that is,
 |
A finite group is nilpotent if and only if its derived group is contained in its Frattini subgroup. For every finite group and every polycyclic group 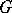 , the group
, the group 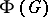 is nilpotent.
is nilpotent.
References
| [1] | G. Frattini, "Intorno alla generazione dei gruppi di operazioni" Atti Accad. Lincei, Rend. (IV) , 1 (1885) pp. 281–285 |
| [2] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
How to Cite This Entry:
Frattini-subgroup(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frattini-subgroup(2)&oldid=11533
Frattini-subgroup(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frattini-subgroup(2)&oldid=11533
This article was adapted from an original article by N.N. Vil'yams (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article