Fractions, ring of
A ring related to a given associative ring 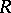 with an identity. The (right classical) ring of fractions of
with an identity. The (right classical) ring of fractions of 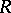 is the ring
is the ring 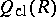 in which every regular element (that is, not a zero divisor) of
in which every regular element (that is, not a zero divisor) of 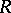 is invertible, and every element of
is invertible, and every element of 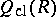 has the form
has the form 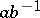 with
with 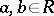 . The ring
. The ring 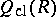 exists if and only if
exists if and only if 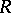 satisfies the right-hand Ore condition (cf. Associative rings and algebras). The maximal (or complete) right ring of fractions of
satisfies the right-hand Ore condition (cf. Associative rings and algebras). The maximal (or complete) right ring of fractions of 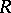 is the ring
is the ring 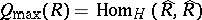 , where
, where 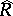 is the injective hull of
is the injective hull of 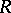 as a right
as a right 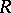 -module, and
-module, and 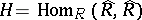 is the endomorphism ring of the right
is the endomorphism ring of the right 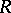 -module
-module 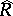 . The ring
. The ring 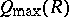 can also be defined as the direct limit
can also be defined as the direct limit
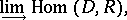 |
where 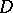 is the set of all dense right ideals of
is the set of all dense right ideals of 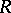 (a right ideal
(a right ideal 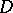 of a ring
of a ring 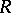 is called a dense ideal if
is called a dense ideal if
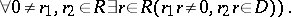 |
References
| [1] | J. Lambek, "Lectures on rings and modules" , Blaisdell (1966) |
| [2] | V.P. Elizarov, "Quotient rings" Algebra and Logic , 8 : 4 (1969) pp. 219–243 Algebra i Logika , 8 : 4 (1969) pp. 381–424 |
| [3] | B. Stenström, "Rings of quotients" , Springer (1975) |
Comments
This notion is also called a ring of quotients.
Fractions, ring of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractions,_ring_of&oldid=17898