Fractional integration and differentiation
An extension of the operations of integration and differentiation to the case of fractional powers. Let 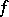 be integrable on the interval
be integrable on the interval 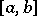 , let
, let 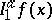 be the integral of
be the integral of 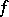 along
along 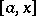 , while
, while 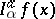 is the integral of
is the integral of 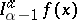 along
along 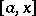 ,
, 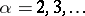 . One then has
. One then has
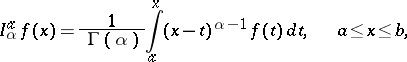 | (1) |
where 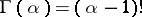 is the gamma-function. The right-hand side makes sense for every
is the gamma-function. The right-hand side makes sense for every 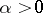 . The relation (1) defines the fractional integral (or the Riemann–Liouville integral) of order
. The relation (1) defines the fractional integral (or the Riemann–Liouville integral) of order 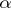 of
of 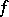 with starting point
with starting point  . The operator
. The operator 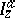 was studied by B. Riemann (1847) for complex values of the parameter
was studied by B. Riemann (1847) for complex values of the parameter  . The operator
. The operator 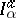 is linear and has the semi-group property:
is linear and has the semi-group property:
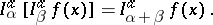 |
The operation inverse to fractional integration is known as fractional differentiation: If 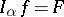 , then
, then 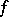 is the fractional derivative of order
is the fractional derivative of order  of
of 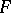 . If
. If 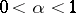 , Marchaut's formula applies:
, Marchaut's formula applies:
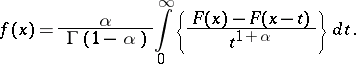 |
The concept of fractional integration and differentiation was first introduced by J. Liouville (1832); he studied, in particular, the operator 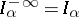 ,
, 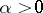 :
:
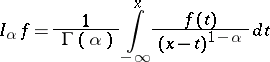 |
(subject to appropriate restrictions on  ; cf. [1], which also contains estimates of the operator
; cf. [1], which also contains estimates of the operator 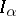 in
in 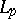 ).
).
The following definition (H. Weyl, 1917) is convenient for an integrable  -periodic function
-periodic function 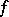 with zero average value over the period. If
with zero average value over the period. If
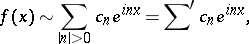 |
then the Weyl integral 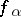 of order
of order 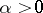 of
of  is defined by the formula
is defined by the formula
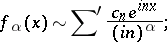 | (2) |
and the derivative 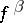 of order
of order 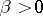 is defined by the equation
is defined by the equation
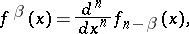 |
where  is the smallest integer larger than
is the smallest integer larger than 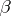 (it should be noted that
(it should be noted that 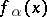 coincides with
coincides with 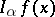 ).
).
These definitions were further developed in the framework of the theory of generalized functions. For periodic generalized functions
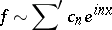 |
the operation of fractional integration 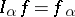 is realized according to formula (2) for all real
is realized according to formula (2) for all real 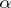 (if
(if 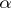 is negative,
is negative, 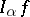 coincides with the partial derivative of order
coincides with the partial derivative of order 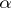 ) and has the semi-group property with respect to the parameter
) and has the semi-group property with respect to the parameter 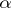 .
.
In an  -dimensional space
-dimensional space 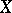 the analogue of the operator of fractional integration is the Riesz potential (or the integral of potential type)
the analogue of the operator of fractional integration is the Riesz potential (or the integral of potential type)
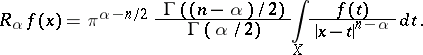 |
The operation inverse to 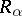 is said to be the Riesz derivative of order
is said to be the Riesz derivative of order 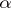 .
.
References
| [1] | G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1934) |
| [2] | A. Zygmund, "Trigonometric series" , 1 , Cambridge Univ. Press (1988) |
| [3] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
| [4] | M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian) |
Fractional integration and differentiation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractional_integration_and_differentiation&oldid=13622