Fraïssé characterization of elementary equivalence
Interpretations for a formal language are equivalent provided that they give the same truth values to sentences in the language. Equivalent interpretations for first-order languages are said to be elementarily equivalent. R. Fraïssé [a2] established a characterization for elementary equivalence that is purely mathematical, in the sense that it does not mention sentences. Unlike the characterizations of S. Kochen [a5] and H.J. Keisler [a4], Fraïssé's characterization applies only to those first-order languages whose non-logical vocabulary is finite and contains no functional constants.
Let 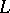 be such a first-order language (with equality). Each predicate constant in the non-logical vocabulary of
be such a first-order language (with equality). Each predicate constant in the non-logical vocabulary of 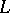 is associated with an unique positive integer called its degree. Let
is associated with an unique positive integer called its degree. Let 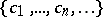 be an infinite set of individual constants not in the non-logical vocabulary of
be an infinite set of individual constants not in the non-logical vocabulary of 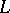 . The family of first-order languages
. The family of first-order languages 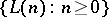 is defined as follows:
is defined as follows:
1) 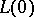 is
is 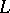 ;
;
2) 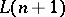 is the language obtained from
is the language obtained from 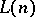 by adding
by adding 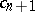 to the non-logical vocabulary of
to the non-logical vocabulary of  .
.
Interpretations for 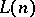 are ordered pairs
are ordered pairs 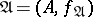 , where
, where 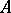 is a non-empty set (the domain of
is a non-empty set (the domain of 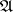 ) and
) and 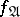 is a function defined on the non-logical vocabulary of
is a function defined on the non-logical vocabulary of 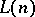 as follows:
as follows:
1) if 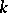 is an individual constant,
is an individual constant, 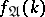 (the denotation of
(the denotation of 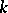 on
on 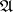 ) is a member of
) is a member of 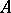 ;
;
2) if 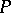 is a predicate constant of degree
is a predicate constant of degree 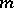 ,
, 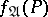 (the extension of
(the extension of 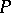 on
on 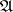 ) is a subset of
) is a subset of 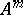 .
.
When 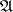 is an interpretation of
is an interpretation of 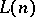 and
and 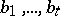 are members of
are members of 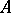 ,
, 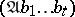 denotes the interpretation of
denotes the interpretation of 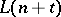 with domain
with domain 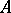 that agrees with
that agrees with 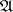 on the non-logical vocabulary of
on the non-logical vocabulary of 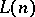 and in which
and in which 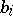 is the denotation of
is the denotation of 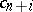 for all
for all 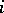 ,
, 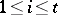 .
.
Given interpretations 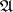 and
and 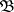 for
for 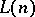 ,
, 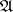 is a sub-interpretation, or subsystem, of
is a sub-interpretation, or subsystem, of 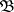 provided that:
provided that:
1) 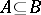 ;
;
2) 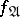 and
and 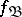 give the same denotations to individual constants of
give the same denotations to individual constants of 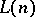 ;
;
3) if 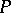 is a predicate constant of degree
is a predicate constant of degree 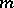 ,
, 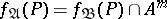 .
.
Let 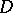 be a subset of
be a subset of 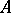 .
. 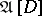 denotes the subsystem of
denotes the subsystem of 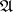 generated by
generated by 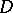 (i.e., the smallest subsystem of
(i.e., the smallest subsystem of 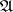 whose domain contains
whose domain contains 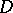 ). When
). When 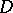 is non-empty,
is non-empty, 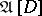 exists and its domain is finite if
exists and its domain is finite if 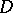 is finite. Let
is finite. Let 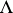 denote the null set.
denote the null set. 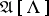 exists when
exists when 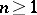 or when
or when 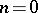 and
and 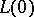 contains individual constants.
contains individual constants.
For each 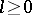 ,
, 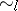 is defined on pairs of interpretations for
is defined on pairs of interpretations for 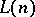 as follows:
as follows:
1) 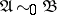 if and only if
if and only if 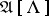 and
and 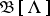 are isomorphic;
are isomorphic;
2) 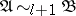 if and only if
if and only if
2a) for all 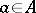 there is a
there is a 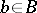 such that
such that 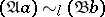 ;
;
2b) for all 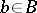 there is an
there is an 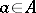 such that
such that 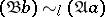 .
.
Fraïssé proved that 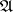 and
and 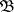 are elementarily equivalent if and only if
are elementarily equivalent if and only if 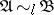 for all
for all 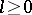 .
.
For 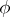 a sentence in
a sentence in 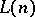 ,
, 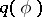 is the number of distinct variables occurring in
is the number of distinct variables occurring in 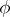 ;
; 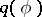 is called the quantifier rank of
is called the quantifier rank of 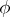 . One writes
. One writes 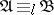 when
when 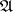 and
and 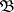 give the same truth values to all sentences in
give the same truth values to all sentences in 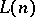 of quantifier rank less than or equal to
of quantifier rank less than or equal to 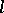 .
. 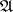 and
and 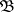 are elementarily equivalent if and only if
are elementarily equivalent if and only if 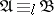 for all
for all 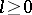 .
.
Let 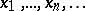 be an enumeration (without repeats) of the individual variables in
be an enumeration (without repeats) of the individual variables in 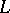 . Fix an enumeration (without repeats) of the formulas in
. Fix an enumeration (without repeats) of the formulas in 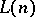 . Let
. Let 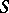 be a non-empty finite set of formulas. There is an
be a non-empty finite set of formulas. There is an 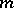 such that
such that 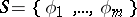 and
and 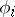 occurs before
occurs before 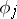 in the enumeration when
in the enumeration when 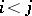 . Let
. Let 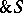 denote
denote 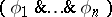 , and let
, and let 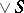 denote
denote 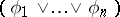 .
.
Given  ,
, 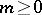 ,
, 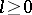 , and a sequence
, and a sequence 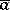 of members of
of members of 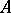 of length
of length 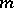 , the formula
, the formula 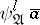 is defined as follows.
is defined as follows. 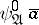 is the conjunction of the set consisting of all atomic formulas in
is the conjunction of the set consisting of all atomic formulas in 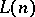 in the variables
in the variables 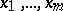 which are satisfied by
which are satisfied by 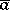 in
in 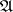 , and of the negations of all such formulas which are not satisfied by
, and of the negations of all such formulas which are not satisfied by 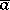 in
in 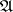 .
. 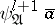 is the conjunction of
is the conjunction of
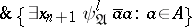 |
and
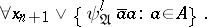 |
Let  denote the null sequence. When
denote the null sequence. When 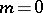 ,
, 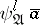 is written
is written 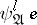 . For fixed
. For fixed 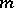 and
and 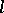 there are only finitely many formulas of the form
there are only finitely many formulas of the form 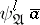 .
. 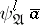 is a formula in
is a formula in 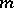 free variables and
free variables and 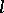 bound variables. Hence
bound variables. Hence 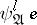 is of quantifier rank
is of quantifier rank 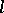 .
.
Assume that 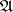 and
and  are interpretations for
are interpretations for 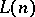 ,
, 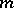 and
and 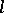 are natural numbers such that
are natural numbers such that 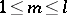 ,
, 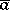 is a sequence of members of
is a sequence of members of 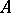 of length
of length 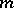 , and
, and 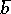 is a sequence of members of
is a sequence of members of 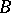 of length
of length 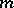 .
. 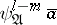 is satisfied by
is satisfied by 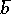 in
in 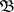 if and only if
if and only if 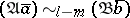 . This result implies that for all
. This result implies that for all 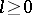 the following assertions are equivalent:
the following assertions are equivalent:
1) 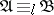 ;
;
2) 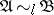 ;
;
3) 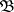 is a model of
is a model of 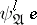 . Fraïssé's characterization is immediate.
. Fraïssé's characterization is immediate.
It also follows that any sentence of quantifier rank less than or equal to 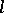 which is true on
which is true on 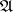 is a logical consequence of
is a logical consequence of 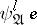 (i.e., true on all models of
(i.e., true on all models of 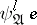 ). Hence every such sentence of its negation is a logical consequence of
). Hence every such sentence of its negation is a logical consequence of 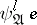 . Since for fixed
. Since for fixed 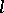 there are only finitely many sentences of the form
there are only finitely many sentences of the form 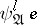 , there are only finitely many non-equivalent sentences of quantifier rank less than or equal to
, there are only finitely many non-equivalent sentences of quantifier rank less than or equal to 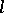 . Let
. Let 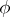 be a sentence of quantifier rank
be a sentence of quantifier rank 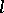 . Assume that
. Assume that 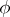 has models. Let
has models. Let 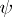 be the sentence
be the sentence
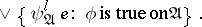 |
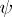 is a distributive normal form in the sense of J. Hintikka [a3]. Furthermore,
is a distributive normal form in the sense of J. Hintikka [a3]. Furthermore, 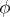 and
and 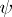 are logically equivalent (i.e., have exactly the same models).
are logically equivalent (i.e., have exactly the same models).
Let 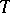 be a set of sentences. Call
be a set of sentences. Call 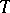 a theory when every logical consequence of
a theory when every logical consequence of 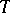 is a member of
is a member of 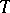 . Assume that
. Assume that 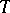 has models. Let
has models. Let
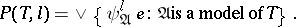 |
Let 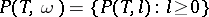 .
. 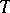 and
and 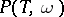 have exactly the same models;
have exactly the same models; 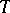 is decidable if and only if
is decidable if and only if 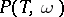 is recursive and
is recursive and 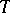 is finitely axiomatizable if and only if there is an
is finitely axiomatizable if and only if there is an 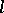 such that the models of
such that the models of 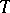 are closed under
are closed under  .
.
Alternative definitions of 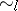 can be found in [a6] and [a7]. A. Ehrenfeucht [a1] independently obtained Fraïssé's characterization formulated in terms of two-person games. Fraïssé's characterization has been extended to provide characterizations of equivalence for a variety of "non-elementary" languages. For example, see [a6], [a7], and [a8].
can be found in [a6] and [a7]. A. Ehrenfeucht [a1] independently obtained Fraïssé's characterization formulated in terms of two-person games. Fraïssé's characterization has been extended to provide characterizations of equivalence for a variety of "non-elementary" languages. For example, see [a6], [a7], and [a8].
References
| [a1] | A. Ehrenfeucht, "An application of games to the completeness problem for formalised theories" Fundam. Math. , 49 (1956) pp. 129–141 |
| [a2] | R. Fraïssé, "Sur quelques classifications des relations basés sur des isomorphismes restraintes" Publ. Sci. Univ. Alger. Ser. A , 2 (1955) pp. 11–60, 273–295 |
| [a3] | J. Hintikka, "Distributive normal forms in first order logic" J.N. Crossley (ed.) M.A.E. Dummet (ed.) , Formal Systems and Recursive Functions , North-Holland (1965) pp. 48–91 |
| [a4] | H.J. Keisler, "Ultraproducts and elementary classes" Indagationes Mathematicae , 23 (1961) pp. 277–295 |
| [a5] | S. Kochen, "Ultraproducts in the theory of models" Ann. of Math. , 74 (1961) pp. 231–261 |
| [a6] | A. Mostowski, "Thirty years of foundational studies" , Barnes and Noble (1966) |
| [a7] | D. Scott, "Logic with denumerably long formulas and finite strings of quantifiers" J.W. Addison (ed.) L. Henkin (ed.) A. Tarski (ed.) , The Theory of Models , North-Holland (1966) pp. 329–341 |
| [a8] | G. Weaver, J. Welaish, "Back and forth arguments in modal logic" J. Symb. Logic , 51 (1987) pp. 969–980 |
Fraïssé characterization of elementary equivalence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fra%C3%AFss%C3%A9_characterization_of_elementary_equivalence&oldid=14766