Frénet trihedron
From Encyclopedia of Mathematics
natural trihedron
The trihedral angle formed by the rays emanating from a point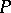 
of a regular curve 
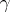in the respective directions of the tangent 
, the normal 
and the binormal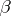 
to the curve. If the 
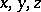coordinate axes, respectively, lie along the sides of the Frénet trihedron, then the equation of the curve in this coordinate system has the form
 |
 |
 |
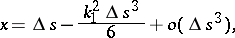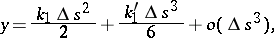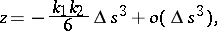where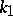 
and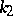 
are the curvature and torsion of the curve, and 
is the natural parameter. The qualitative form of the projections of the curve onto the planes of the Frénet trihedron for 
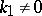and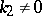 
can be seen in the figures.
Figure: f041700a
Figure: f041700b
Figure: f041700c
This trihedron was studied by F. Frénet (1847).
Comments
References
| [a1] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 |
How to Cite This Entry:
Frénet trihedron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9net_trihedron&oldid=13524
Frénet trihedron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9net_trihedron&oldid=13524
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article