Fréchet topology
The topological structure (topology) of an 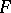 -space (a space of type
-space (a space of type 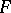 ; cf. also Fréchet space), i.e. a completely metrizable topological vector space. The term was introduced by S. Banach in honour of M. Fréchet. Many authors, however, demand additionally local convexity. A complete topological vector space is an
; cf. also Fréchet space), i.e. a completely metrizable topological vector space. The term was introduced by S. Banach in honour of M. Fréchet. Many authors, however, demand additionally local convexity. A complete topological vector space is an 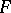 -space if and only if it has a countable basis of neighbourhoods of the origin. The topology of an
-space if and only if it has a countable basis of neighbourhoods of the origin. The topology of an 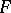 -space
-space 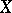 can be given by means of an
can be given by means of an 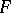 -norm, i.e. a function
-norm, i.e. a function 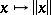 satisfying:
satisfying:
i) 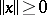 and
and  if and only if
if and only if 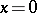 ;
;
ii) 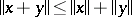 for all
for all 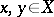 ;
;
iii) for each scalar 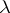 ,
, 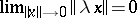 , and for each
, and for each 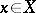 ,
, 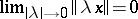 . This means that the (complete) topology of
. This means that the (complete) topology of 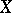 can be given by means of a distance of the form
can be given by means of a distance of the form 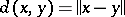 . The completion of any metrizable topological vector space (cf. Completion) is an
. The completion of any metrizable topological vector space (cf. Completion) is an 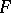 -space and, consequently, the topology of any metric vector space can be given by means of a translation-invariant distance. Without loss of generality it can be assumed that
-space and, consequently, the topology of any metric vector space can be given by means of a translation-invariant distance. Without loss of generality it can be assumed that 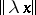 depends only upon
depends only upon 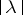 and that the function
and that the function 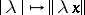 is non-decreasing for each
is non-decreasing for each 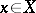 . If one relaxes condition i) so that
. If one relaxes condition i) so that  can hold for a non-zero
can hold for a non-zero  , one obtains an
, one obtains an 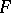 -semi-norm. The topology of an arbitrary topological vector space can be given by means of a family of
-semi-norm. The topology of an arbitrary topological vector space can be given by means of a family of 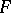 -semi-norms; consequently, every complete topological vector space is an inverse (projective) limit of a directed family of
-semi-norms; consequently, every complete topological vector space is an inverse (projective) limit of a directed family of 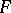 -spaces.
-spaces.
Important classes of 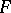 -spaces.
-spaces.
Locally convex 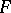 -spaces.
-spaces.
Such spaces are also called spaces of type 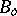 (some authors call them just Fréchet spaces, but see Fréchet space). The topology of such a space
(some authors call them just Fréchet spaces, but see Fréchet space). The topology of such a space 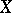 can be given by means of an increasing sequence of (homogeneous) semi-norms
can be given by means of an increasing sequence of (homogeneous) semi-norms
 | (a1) |
so that a sequence  of elements of
of elements of  tends to
tends to  if and only if
if and only if 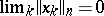 for
for 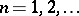 . An
. An 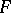 -norm giving this topology can be written as
-norm giving this topology can be written as
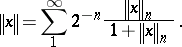 |
If 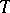 is a continuous linear operator from a
is a continuous linear operator from a 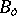 -space
-space  to a
to a 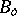 -space
-space 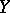 , then for each
, then for each  there are a
there are a 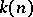 and a
and a 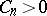 such that
such that  ,
, 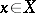 , for all
, for all  (it is important here that the systems of semi-norms giving, respectively, the topologies of
(it is important here that the systems of semi-norms giving, respectively, the topologies of 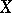 and
and 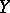 satisfy (a1)). The dual space
satisfy (a1)). The dual space 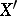 of a
of a 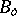 -space
-space 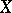 (the space of all continuous linear functionals provided with the topology of uniform convergence on bounded sets) is said to be an
(the space of all continuous linear functionals provided with the topology of uniform convergence on bounded sets) is said to be an 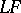 -space; it is non-metrizable (unless
-space; it is non-metrizable (unless 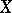 is a Banach space). Any space of type
is a Banach space). Any space of type  is an inverse (projective) limit of a sequence of Banach spaces.
is an inverse (projective) limit of a sequence of Banach spaces.
Complete locally bounded spaces.
A topological vector space 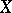 is said to be locally bounded if it has a bounded neighbourhood of the origin (then it has a basis of such neighbourhoods consisting of bounded sets). The topology of such a space
is said to be locally bounded if it has a bounded neighbourhood of the origin (then it has a basis of such neighbourhoods consisting of bounded sets). The topology of such a space 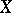 is metrizable and can be given by means of a
is metrizable and can be given by means of a 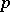 -homogeneous norm,
-homogeneous norm, 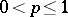 , i.e. an
, i.e. an 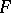 -norm satisfying instead of iii) the more restrictive condition
-norm satisfying instead of iii) the more restrictive condition
iiia) 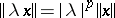 for all scalars
for all scalars 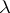 and all
and all 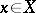 .
.
For this reason, locally bounded spaces are sometimes called  -normed spaces. The class of all Banach spaces is exactly the intersection of the class of locally convex
-normed spaces. The class of all Banach spaces is exactly the intersection of the class of locally convex 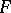 -spaces and the class of complete locally bounded spaces. The dual space of a locally bounded space can be trivial, i.e. consist only of a zero functional.
-spaces and the class of complete locally bounded spaces. The dual space of a locally bounded space can be trivial, i.e. consist only of a zero functional.
Locally pseudo-convex 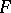 -spaces.
-spaces.
They are like 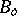 -spaces, but with
-spaces, but with 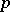 -homogeneous semi-norms instead of homogeneous semi-norms (the exponent
-homogeneous semi-norms instead of homogeneous semi-norms (the exponent 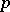 may depend upon the semi-norm). This class contains the class of locally convex
may depend upon the semi-norm). This class contains the class of locally convex 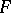 -spaces and the class of complete locally bounded spaces.
-spaces and the class of complete locally bounded spaces.
Examples of 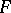 -spaces.
-spaces.
The space 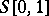 of all Lebesgue-measurable functions on the unit interval with the topology of convergence in measure (asymptotic convergence) is a space of type
of all Lebesgue-measurable functions on the unit interval with the topology of convergence in measure (asymptotic convergence) is a space of type 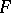 . Its topology can be given by the
. Its topology can be given by the 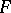 -norm
-norm
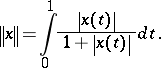 |
This space is not locally pseudo-convex.
The space 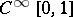 of all infinitely differentiable functions on the unit interval with the topology of unform convergence of functions together with all derivatives is a
of all infinitely differentiable functions on the unit interval with the topology of unform convergence of functions together with all derivatives is a 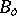 -space. Its topology can be given by semi-norms
-space. Its topology can be given by semi-norms
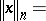 |
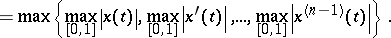 |
The space 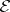 of all entire functions of one complex variable with the topology of uniform convergence on compact subsets of the complex plane is a
of all entire functions of one complex variable with the topology of uniform convergence on compact subsets of the complex plane is a 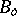 -space. Its topology can be given by the semi-norms
-space. Its topology can be given by the semi-norms
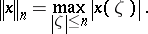 |
The space 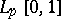 on the unit interval,
on the unit interval, 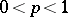 , is a complete locally bounded space with trivial dual. Its topology can be given by
, is a complete locally bounded space with trivial dual. Its topology can be given by 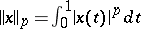 (its discrete analogue, the space
(its discrete analogue, the space  of all sequences summable with the
of all sequences summable with the 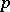 -th power, has a non-trivial dual).
-th power, has a non-trivial dual).
The space 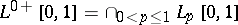 with the semi-norms
with the semi-norms 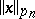 , where
, where 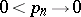 , is a locally pseudo-convex space of type
, is a locally pseudo-convex space of type 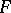 which is not locally bounded.
which is not locally bounded.
General facts about  -spaces.
-spaces.
A linear operator between 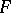 spaces is continuous if and only if it maps bounded sets onto bounded sets.
spaces is continuous if and only if it maps bounded sets onto bounded sets.
Let  be a family of continuous linear operators from an
be a family of continuous linear operators from an 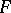 -space
-space 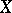 to an
to an 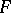 -space space
-space space 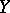 . If the set
. If the set 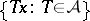 is bounded in
is bounded in 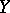 for each fixed
for each fixed 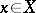 , then
, then 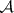 is equicontinuous (the Mazur–Orlicz theorem; it is a theorem of Banach–Steinhaus type, cf. also Banach–Steinhaus theorem).
is equicontinuous (the Mazur–Orlicz theorem; it is a theorem of Banach–Steinhaus type, cf. also Banach–Steinhaus theorem).
If 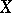 and
and 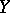 are
are 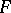 -spaces and
-spaces and 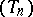 is a sequence of continuous linear operators from
is a sequence of continuous linear operators from 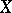 to
to 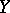 such that for each
such that for each 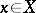 the limit
the limit 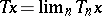 exists, then
exists, then 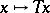 is a continuous linear operator from
is a continuous linear operator from 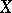 to
to 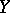 .
.
The image of an open set under a continuous linear operator between 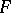 -spaces is open (the open mapping theorem).
-spaces is open (the open mapping theorem).
The graph of a linear operator 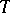 between
between 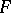 -spaces is closed if and only if
-spaces is closed if and only if 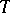 is continuous (the closed graph theorem).
is continuous (the closed graph theorem).
If a one-to-one continuous linear operator maps an 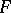 -space onto an
-space onto an 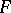 -space, then the inverse operator is continuous (the inverse operator theorem).
-space, then the inverse operator is continuous (the inverse operator theorem).
A separately continuous bilinear mapping between 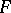 -spaces is jointly continuous (cf. also Continuous function).
-spaces is jointly continuous (cf. also Continuous function).
References
| [a1] | S. Banach, "Théorie des operations lineaires" , Warszawa (1932) |
| [a2] | N. Bourbaki, "Espaces vectorielles topologiques" , Paris (1981) pp. Chapt. 1–5 |
| [a3] | N. Dunford, J.T. Schwartz, "Linear operators" , I. General theory , Wiley, reprint (1988) |
| [a4] | A. Grothendieck, "Topological vector spaces" , New York (1973) |
| [a5] | H. Jarchow, "Locally convex spaces" , Teubner (1981) |
| [a6] | G. Köthe, "Topological vector spaces" , I–II , New York (1969–1979) |
| [a7] | S. Rolewicz, "Metric linear spaces" , PWN & Reidel (1972) |
| [a8] | H.H. Schaefer, "Topological vector spaces" , Springer (1971) |
| [a9] | L. Waelbroeck, "Topological vector spaces and algebras" , Lecture Notes in Mathematics , 230 , Springer (1971) |
| [a10] | A. Wilansky, "Modern methods in topological vector spaces" , New York (1978) |
Fréchet topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9chet_topology&oldid=12759