Fourier transform, discrete
A transform used for the harmonic analysis of functions given on a discrete set of points.
If a function is given on the set of points  by its values
by its values  ,
,  ,
,  , where
, where 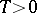 is the period of the function, then the discrete Fourier transform of the vector
is the period of the function, then the discrete Fourier transform of the vector  is the vector
is the vector  , where
, where  is the matrix with entries
is the matrix with entries
 |
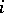 is the imaginary unit,
is the imaginary unit, 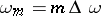 ,
, 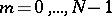 ,
,  . The components of the vector
. The components of the vector 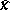 are analogues of the Fourier coefficients in the usual trigonometric expansions. The discrete Fourier transform is used to calculate approximately these coefficients, spectra, auto- and mutual-correlation functions, etc. A direct computation of the discrete Fourier transform requires about
are analogues of the Fourier coefficients in the usual trigonometric expansions. The discrete Fourier transform is used to calculate approximately these coefficients, spectra, auto- and mutual-correlation functions, etc. A direct computation of the discrete Fourier transform requires about  arithmetic operations and a great expenditure of machine time. The method of the fast Fourier transform (see [1]) enables one to reduce the number of operations considerably. When
arithmetic operations and a great expenditure of machine time. The method of the fast Fourier transform (see [1]) enables one to reduce the number of operations considerably. When 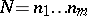 , this method carries out the discrete Fourier transform approximately in
, this method carries out the discrete Fourier transform approximately in 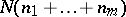 operations, increasing the accuracy of the calculation. When
operations, increasing the accuracy of the calculation. When 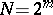 there are algorithms which are particularly convenient in practice. There is a considerable number of programs realizing or using the fast Fourier transform to solve applied problems. The method of the fast Fourier transform includes widely known efficient methods for computing the discrete Fourier transform, for example, the Runge method (see [2] and Runge–Kutta method).
there are algorithms which are particularly convenient in practice. There is a considerable number of programs realizing or using the fast Fourier transform to solve applied problems. The method of the fast Fourier transform includes widely known efficient methods for computing the discrete Fourier transform, for example, the Runge method (see [2] and Runge–Kutta method).
References
| [1] | J. Cooley, J. Tukey, "An algorithm for the machine calculation of complex Fourier series" Math. Comp. , 19 (1965) pp. 297–301 |
| [2] | C.Z. Runge, Math. Phys. , 48 (1903) pp. 443 |
Comments
The fast Fourier transform of J. Cooley and J. Tukey exploits the special structure of the matrix  . For
. For 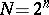 it turns out that the matrix
it turns out that the matrix 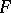 can be factorized into
can be factorized into  matrices the rows of which contain only a few non-zero entries, the non-zero entries being equal or having opposite signs. For example, if
matrices the rows of which contain only a few non-zero entries, the non-zero entries being equal or having opposite signs. For example, if 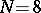 , then
, then 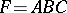 where the rows of the factor matrices
where the rows of the factor matrices 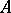 ,
, 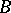 and
and 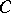 each contain only 2 non-zero elements
each contain only 2 non-zero elements  and
and 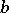 such that either
such that either 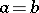 or
or 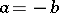 (written out formulas for the case
(written out formulas for the case  can be found in [a1], p. 255). Thus, the computation of the vector
can be found in [a1], p. 255). Thus, the computation of the vector 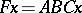 requires only
requires only 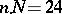 instead of
instead of 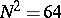 "operations" . A detailed theoretical treatment of the fast Fourier transform as well as algorithmic information is provided by the monograph [a2].
"operations" . A detailed theoretical treatment of the fast Fourier transform as well as algorithmic information is provided by the monograph [a2].
References
| [a1] | C.E. Fröberg, "Introduction to numerical analysis, theory and applications" , Benjamin/Cummings (1985) |
| [a2] | E.D. Brigham, "The fast Fourier transform" , Prentice-Hall (1974) |
| [a3] | R.W. Ramirez, "The FFT fundamentals and concepts" , Prentice-Hall (1985) |
| [a4] | D.F. Elliot, K.R. Rao, "Fast transforms: algorithms, analysis, applications" , Acad. Press (1982) |
Fourier transform, discrete. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_transform,_discrete&oldid=16930