Fourier series in orthogonal polynomials
A series of the form
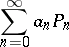 | (1) |
where the polynomials 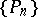 are orthonormal on an interval
are orthonormal on an interval 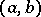 with weight function
with weight function  (see Orthogonal polynomials) and the coefficients
(see Orthogonal polynomials) and the coefficients 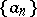 are calculated from the formula
are calculated from the formula
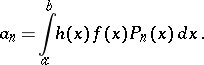 | (2) |
Here, the function 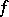 belongs to the class
belongs to the class  of functions that are square summable (Lebesgue integrable) with weight function
of functions that are square summable (Lebesgue integrable) with weight function  over the interval
over the interval 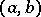 of orthogonality.
of orthogonality.
As for any orthogonal series, the partial sums 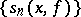 of (1) are the best-possible approximations to
of (1) are the best-possible approximations to 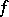 in the metric of
in the metric of 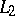 and satisfy the condition
and satisfy the condition
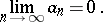 | (3) |
For a proof of the convergence of the series (1) at a single point  or on a certain set in
or on a certain set in 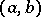 one usually applies the equality
one usually applies the equality
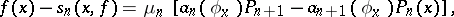 |
where 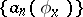 are the Fourier coefficients of an auxiliary function
are the Fourier coefficients of an auxiliary function 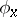 , given by
, given by
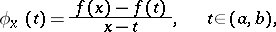 |
for fixed  , and
, and 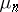 is the coefficient given by the Christoffel–Darboux formula. If the interval of orthogonality
is the coefficient given by the Christoffel–Darboux formula. If the interval of orthogonality 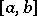 is bounded, if
is bounded, if 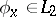 and if the sequence
and if the sequence 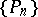 is bounded at the given point
is bounded at the given point  , then the series (1) converges to the value
, then the series (1) converges to the value 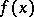 .
.
The coefficients (2) can also be defined for a function 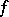 in the class
in the class  , that is, for functions that are summable with weight function
, that is, for functions that are summable with weight function 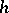 over
over 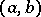 . For a bounded interval
. For a bounded interval 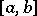 , condition (3) holds if
, condition (3) holds if 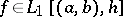 and if the sequence
and if the sequence 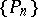 is uniformly bounded on the whole interval
is uniformly bounded on the whole interval 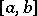 . Under these conditions the series (1) converges at a certain point
. Under these conditions the series (1) converges at a certain point  to the value
to the value 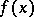 if
if 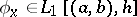 .
.
Let 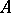 be a part of
be a part of 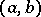 on which the sequence
on which the sequence 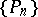 is uniformly bounded, let
is uniformly bounded, let 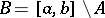 and let
and let 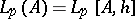 be the class of functions that are
be the class of functions that are 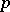 -summable over
-summable over 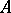 with weight function
with weight function 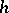 . If, for a fixed
. If, for a fixed 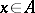 , one has
, one has 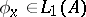 and
and 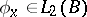 , then the series (1) converges to
, then the series (1) converges to 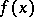 .
.
For the series (1) the localization principle for conditions of convergence holds: If two functions 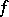 and
and 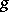 in
in 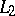 coincide in an interval
coincide in an interval 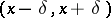 , where
, where 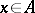 , then the Fourier series of these two functions in the orthogonal polynomials converge or diverge simultaneously at
, then the Fourier series of these two functions in the orthogonal polynomials converge or diverge simultaneously at  . An analogous assertion is valid if
. An analogous assertion is valid if 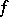 and
and 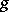 belong to
belong to 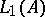 and
and 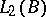 and
and 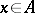 .
.
For the classical orthogonal polynomials the theorems on the equiconvergence with a certain associated trigonometric Fourier series hold for the series (1) (see Equiconvergent series).
Uniform convergence of the series (1) over the whole bounded interval of orthogonality 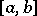 , or over part of it, is usually investigated using the Lebesgue inequality
, or over part of it, is usually investigated using the Lebesgue inequality
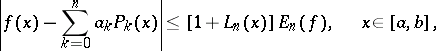 |
where the Lebesgue function
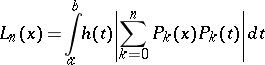 |
does not depend on 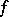 and
and 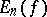 is the best uniform approximation (cf. Best approximation) to the continuous function
is the best uniform approximation (cf. Best approximation) to the continuous function 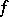 on
on 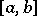 by polynomials of degree not exceeding
by polynomials of degree not exceeding  . The sequence of Lebesgue functions
. The sequence of Lebesgue functions 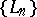 can grow at various rates at the various points of
can grow at various rates at the various points of  , depending on the properties of
, depending on the properties of  . However, for the whole interval
. However, for the whole interval 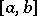 one introduces the Lebesgue constants
one introduces the Lebesgue constants
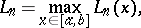 |
which increase unboundedly as 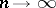 (for different systems of orthogonal polynomials the Lebesgue constants can increase at different rates). The Lebesgue inequality implies that if the condition
(for different systems of orthogonal polynomials the Lebesgue constants can increase at different rates). The Lebesgue inequality implies that if the condition
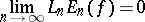 |
is satisfied, then the series (1) converges uniformly to 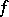 on the whole interval
on the whole interval 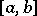 . On the other hand, the rate at which the sequence
. On the other hand, the rate at which the sequence 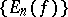 tends to zero depends on the differentiability properties of
tends to zero depends on the differentiability properties of 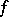 . Thus, in many cases it is not difficult to formulate sufficient conditions for the right-hand side of the Lebesgue inequality to tend to zero as
. Thus, in many cases it is not difficult to formulate sufficient conditions for the right-hand side of the Lebesgue inequality to tend to zero as 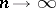 (see, for example, Legendre polynomials; Chebyshev polynomials; Jacobi polynomials). In the general case of an arbitrary weight function one can obtain specific results if one knows asymptotic formulas or bounds for the orthogonal polynomials under consideration.
(see, for example, Legendre polynomials; Chebyshev polynomials; Jacobi polynomials). In the general case of an arbitrary weight function one can obtain specific results if one knows asymptotic formulas or bounds for the orthogonal polynomials under consideration.
References
| [1] | G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975) |
| [2] | Ya.L. Geronimus, "Polynomials orthogonal on a circle and interval" , Pergamon (1960) (Translated from Russian) |
| [3] | P.K. Suetin, "Classical orthogonal polynomials" , Moscow (1979) (In Russian) |
See also the references to Orthogonal polynomials.
Comments
See also [a1], Chapt. 4 and [a2], part one. Equiconvergence theorems have been proved more generally for the case of orthogonal polynomials with respect to a weight function 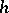 on a finite interval belonging to the Szegö class, i.e.
on a finite interval belonging to the Szegö class, i.e. 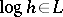 , cf. [a2], Sect. 4.12. For Fourier series in orthogonal polynomials with respect to a weight function on an unbounded interval see [a2], part two.
, cf. [a2], Sect. 4.12. For Fourier series in orthogonal polynomials with respect to a weight function on an unbounded interval see [a2], part two.
References
| [a1] | G. Freud, "Orthogonal polynomials" , Pergamon (1971) (Translated from German) |
| [a2] | P. Nevai, G. Freud, "Orthogonal polynomials and Christoffel functions (A case study)" J. Approx. Theory , 48 (1986) pp. 3–167 |
Fourier series in orthogonal polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_series_in_orthogonal_polynomials&oldid=13878