Fourier coefficients
From Encyclopedia of Mathematics
The coefficients
 | (*) |
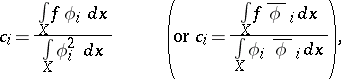in the expansion of a function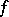 
defined on a space 
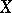with respect to an orthogonal system of real-valued (complex-valued) functions on 
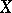. If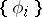 
is an orthogonal system in a Hilbert (pre-Hilbert) space, then, given an element 
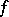of this space, the numbers 
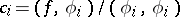are also called the Fourier coefficients of 
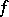with respect to the system 
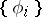. J. Fourier first investigated trigonometric series with coefficients defined by (*).
References
| [1] | S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951) |
How to Cite This Entry:
Fourier coefficients. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_coefficients&oldid=17816
Fourier coefficients. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_coefficients&oldid=17816
This article was adapted from an original article by T.P. Lukashenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article