Difference between revisions of "Fourier-Bessel series"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Fourier–Bessel series to Fourier-Bessel series: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
The expansion of a function 
in a series
 | (*) |
where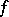 
is a function given on the interval 
, 
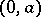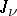is the Bessel function of order 
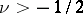(cf. Bessel functions), and the 
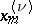are the positive zeros of 
taken in increasing order; the coefficients 
have the following values:
 |
If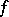 
is a piecewise-continuous function given on an interval 
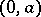and if the integral
 |
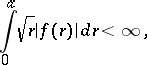then the Fourier–Bessel series converges and its sum is equal to 
at each interior point 
of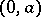 
at which 
locally has bounded variation.
How to Cite This Entry:
Fourier-Bessel series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier-Bessel_series&oldid=19087
Fourier-Bessel series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier-Bessel_series&oldid=19087
This article was adapted from an original article by L.N. Karmazina (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article