Four-dimensional manifold
A topological space in which each point has a neighbourhood homeomorphic to the four-dimensional Euclidean space 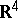 or to the closed half-space
or to the closed half-space 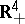 . This definition is usually extended by the requirement that a four-dimensional manifold be Hausdorff as a topological space, and have a countable base. The topology of four-dimensional manifolds occupies a special place in the topology of manifolds. On the one hand, the dimension 4 is too small for the straightforward application of techniques of general position; transversality (and surgery), which are so productive in higher-dimensional topology, yet sufficiently large to exclude the direct use of the more intuitive methods of three-dimensional topology. On the other hand, the topology of four-dimensional manifolds inherits many of the difficulties of three-dimensional and also of higher-dimensional topology. This is illustrated, for example, by the facts that the boundary of a four-dimensional manifold may be an arbitrary three-dimensional manifold, and that every finitely-presented group is the fundamental group of some closed four-dimensional manifold. On the latter observation is based the impossibility of algorithmically recognizing homeomorphy of four-dimensional manifolds. The exceptional status of dimension 4 is well-illustrated by the following fact: There exists a non-standard piecewise-linear (and differentiable) structure on the manifold
. This definition is usually extended by the requirement that a four-dimensional manifold be Hausdorff as a topological space, and have a countable base. The topology of four-dimensional manifolds occupies a special place in the topology of manifolds. On the one hand, the dimension 4 is too small for the straightforward application of techniques of general position; transversality (and surgery), which are so productive in higher-dimensional topology, yet sufficiently large to exclude the direct use of the more intuitive methods of three-dimensional topology. On the other hand, the topology of four-dimensional manifolds inherits many of the difficulties of three-dimensional and also of higher-dimensional topology. This is illustrated, for example, by the facts that the boundary of a four-dimensional manifold may be an arbitrary three-dimensional manifold, and that every finitely-presented group is the fundamental group of some closed four-dimensional manifold. On the latter observation is based the impossibility of algorithmically recognizing homeomorphy of four-dimensional manifolds. The exceptional status of dimension 4 is well-illustrated by the following fact: There exists a non-standard piecewise-linear (and differentiable) structure on the manifold 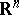 only for
only for 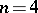 . There exist four-dimensional manifolds that do not admit piecewise-linear structures. If such a structure exists at all, then there is a unique differentiable structure compatible with it. A four-dimensional manifold equipped with a complex structure is called an analytic surface.
. There exist four-dimensional manifolds that do not admit piecewise-linear structures. If such a structure exists at all, then there is a unique differentiable structure compatible with it. A four-dimensional manifold equipped with a complex structure is called an analytic surface.
To every closed orientable four-dimensional manifold 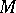 a unimodular integer-valued symmetric bilinear form
a unimodular integer-valued symmetric bilinear form 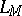 is associated, acting on the free part of the group
is associated, acting on the free part of the group 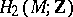 via the intersections of cycles. The signature of this form is called the signature of the manifold. The intersection form is the most important invariant of a four-dimensional manifold. Two closed simply-connected differentiable four-dimensional manifolds are
via the intersections of cycles. The signature of this form is called the signature of the manifold. The intersection form is the most important invariant of a four-dimensional manifold. Two closed simply-connected differentiable four-dimensional manifolds are 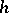 -cobordant (cf.
-cobordant (cf. 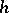 -cobordism) if and only if their forms are isomorphic. If the quadratic form corresponding to the bilinear form
-cobordism) if and only if their forms are isomorphic. If the quadratic form corresponding to the bilinear form 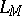 of a differentiable four-dimensional manifold
of a differentiable four-dimensional manifold 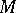 takes only even values, then the structure group SO of its stable tangent bundle can be replaced by the group Spin. Such four-dimensional manifolds are called spin manifolds. There is a topological classification of closed simply-connected four-dimensional manifolds. Every such four-dimensional manifold with an even form is completely determined by it, and every even, integer-valued, symmetric unimodular form is realized as the intersection form of a simply-connected four-dimensional topological manifold. In particular, the four-dimensional topological Poincaré conjecture is true. A classifying invariant of four-dimensional manifolds with odd form is given by pairs of the form
takes only even values, then the structure group SO of its stable tangent bundle can be replaced by the group Spin. Such four-dimensional manifolds are called spin manifolds. There is a topological classification of closed simply-connected four-dimensional manifolds. Every such four-dimensional manifold with an even form is completely determined by it, and every even, integer-valued, symmetric unimodular form is realized as the intersection form of a simply-connected four-dimensional topological manifold. In particular, the four-dimensional topological Poincaré conjecture is true. A classifying invariant of four-dimensional manifolds with odd form is given by pairs of the form 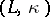 , where
, where 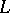 is an odd, integer-valued, symmetric unimodular bilinear form and
is an odd, integer-valued, symmetric unimodular bilinear form and 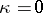 or 1. Every closed simply-connected four-dimensional manifold
or 1. Every closed simply-connected four-dimensional manifold 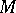 with an odd form is completely determined by the pair
with an odd form is completely determined by the pair 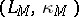 , where
, where 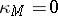 if the stable tangent bundle of the manifold
if the stable tangent bundle of the manifold 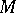 admits a trivialization, and 1 otherwise. Every such pair is realizable. The question of which forms can be realized by simply-connected differentiable four-dimensional manifolds has not yet been completely answered. It is known that all odd indefinite forms can be realized. Among the even indefinite forms, connected sums of the Kummer surface and the manifold
admits a trivialization, and 1 otherwise. Every such pair is realizable. The question of which forms can be realized by simply-connected differentiable four-dimensional manifolds has not yet been completely answered. It is known that all odd indefinite forms can be realized. Among the even indefinite forms, connected sums of the Kummer surface and the manifold 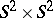 realize
realize 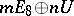 , if
, if 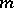 is even and
is even and 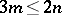 . A form of this type with an odd number
. A form of this type with an odd number 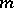 is known not to be the intersection form of a closed differentiable four-dimensional manifold, since the signatures of such spin manifolds are necessarily divisible by 16, while the signature of the form
is known not to be the intersection form of a closed differentiable four-dimensional manifold, since the signatures of such spin manifolds are necessarily divisible by 16, while the signature of the form 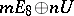 is equal to
is equal to 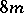 . From the forms given above, only the forms that are given by unit matrices can be realized.
. From the forms given above, only the forms that are given by unit matrices can be realized.
References
| [1] | R. Mandelbaum, "Four-dimensional topology: an introduction" Bull. Amer. Math. Soc. , 2 (1980) pp. 1–159 |
| [2] | M.H. Freedman, "The topology of four-dimensional manifolds" J. Differential Geom. , 17 (1982) pp. 357–453 |
Comments
As noted above, the dimension 4 is rather anomalous from several points of view. For piecewise-linear topology that is illustrated by Rokhlin's theorem: Let 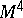 be a compact oriented piecewise-linear manifold with second Stiefel–Whitney class
be a compact oriented piecewise-linear manifold with second Stiefel–Whitney class 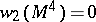 . Then the signature
. Then the signature 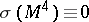
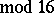 .
.
References
| [a1] | S.K. Donaldson, "An application of gauge theory to four-dimensional topology" J. Differential Geom. , 18 (1983) pp. 279–315 |
| [a2] | D.S. Freed, K.K. Uhlenbeck, "Instantons and four-manifolds" , Springer (1984) |
Four-dimensional manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Four-dimensional_manifold&oldid=15430