Formalization method
A way of expressing by a formal system a mathematical theory. It is one of the main methods in proof theory.
An application of the formalization method involves carrying out the following stages.
1) Putting the original mathematical theory into symbols. In this all the propositions of the theory are written in a suitable logico-mathematical language  .
.
2) The deductive analysis of the theory and the choice of axioms, that is, of a collection of propositions of the theory from which all other propositions of the theory can be logically derived.
3) Adding the axioms in their symbolic notation to a suitable logical calculus based on 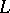 .
.
The system obtained by this formalization is now itself the object of precise mathematical study (see Axiomatic method; Proof theory).
References
| [1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
Formalization method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Formalization_method&oldid=17646