Formal power series
over a ring 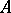 in commuting variables
in commuting variables 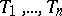
An algebraic expression of the form
 |
where 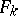 is a form of degree
is a form of degree 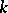 in
in 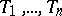 with coefficients in
with coefficients in 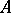 . The minimal value of
. The minimal value of 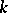 for which
for which 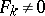 is called the order of the series
is called the order of the series 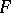 , and the form
, and the form 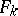 is called the initial form of the series.
is called the initial form of the series.
If
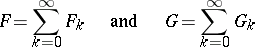 |
are two formal power series, then, by definition,
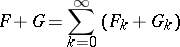 |
and
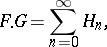 |
where
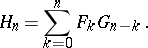 |
The set 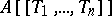 of all formal power series forms a ring under these operations.
of all formal power series forms a ring under these operations.
A polynomial 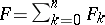 , where
, where 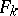 is a form of degree
is a form of degree 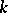 , is identified with the formal power series
, is identified with the formal power series 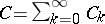 , where
, where 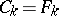 for
for 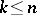 and
and 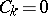 for
for 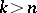 . This defines an imbedding
. This defines an imbedding 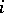 of the polynomial ring
of the polynomial ring 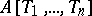 into
into 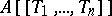 . There is a topology defined on
. There is a topology defined on 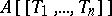 for which the ideals
for which the ideals
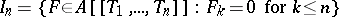 |
form a fundamental system of neighbourhoods of zero. This topology is separable, the ring 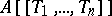 is complete relative to it, and the image of
is complete relative to it, and the image of 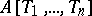 under the imbedding
under the imbedding 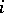 is everywhere dense in
is everywhere dense in 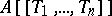 . Relative to this topology, a power series
. Relative to this topology, a power series 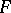 is the limit of its partial sums
is the limit of its partial sums 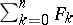 .
.
Suppose that 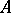 is a commutative ring with an identity. Then so is
is a commutative ring with an identity. Then so is 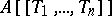 . If
. If 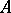 is an integral domain, then so is
is an integral domain, then so is 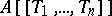 . A formal power series
. A formal power series 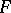 is invertible in
is invertible in 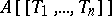 if and only if
if and only if 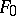 is invertible in
is invertible in 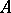 . If
. If  is Noetherian, then so is
is Noetherian, then so is 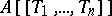 . If
. If 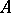 is a local ring with maximal ideal
is a local ring with maximal ideal 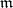 , then
, then 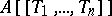 is a local ring with maximal ideal
is a local ring with maximal ideal 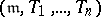 .
.
If a local ring 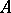 is separable and complete in the
is separable and complete in the 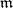 -adic topology, then the Weierstrass preparation theorem is true in
-adic topology, then the Weierstrass preparation theorem is true in 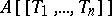 . Let
. Let 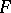 be a formal power series such that for some
be a formal power series such that for some 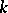 the form
the form 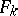 contains a term
contains a term 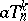 , where
, where 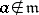 , and let
, and let 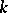 be the minimal index with this property. Then
be the minimal index with this property. Then 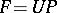 , where
, where 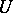 is an invertible formal power series and
is an invertible formal power series and 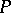 is a polynomial of the form
is a polynomial of the form 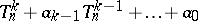 , where the coefficients
, where the coefficients 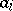 belong to the maximal ideal of
belong to the maximal ideal of 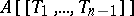 . The elements
. The elements 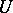 and
and 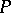 are uniquely determined by
are uniquely determined by 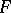 .
.
The ring of formal power series over a field or a discretely-normed ring is factorial.
Rings of formal power series in non-commuting variables have also been studied.
References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [2] | O. Zariski, P. Samuel, "Commutative algebra" , 2 , v. Nostrand (1960) |
Comments
Power series in non-commuting variables are becoming rapidly more important and find applications in combinatorics (enumerative graph theory), computer science (automata) and system and control theory (representation of the input-output behaviour of non-linear systems, especially bilinear systems); cf. the collection [a1] for a first idea.
Let 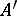 be a ring containing
be a ring containing 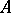 (or provided with a ring homomorphism
(or provided with a ring homomorphism 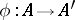 ), let
), let 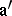 be an ideal in
be an ideal in 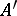 and suppose that
and suppose that 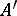 is complete in the
is complete in the 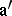 -adic topology on
-adic topology on 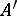 . Let
. Let  be elements of
be elements of 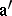 . Then an expression
. Then an expression
 |
where the 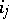 range over
range over 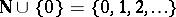 ,
, 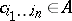 , has a well-defined meaning in
, has a well-defined meaning in 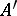 (as the unique limit of the finite sums
(as the unique limit of the finite sums
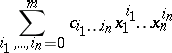 |
as 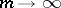 ). Such an expression is also called a formal power series over
). Such an expression is also called a formal power series over 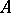 . Mapping
. Mapping 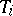 to
to 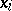 ,
, 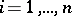 , defines a (continuous) homomorphism
, defines a (continuous) homomorphism 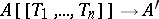 . If this homomorphism is injective, the
. If this homomorphism is injective, the  are said to be analytically independent over
are said to be analytically independent over 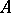 .
.
Let now 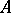 be a field with a multiplicative norm on it (i.e.
be a field with a multiplicative norm on it (i.e.  ), e.g.
), e.g. 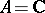 with the usual norm or
with the usual norm or 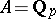 , the rational field, with the norm
, the rational field, with the norm 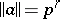 if
if 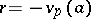 , where
, where 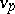 is the
is the 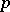 -adic valuation on
-adic valuation on 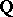 (
(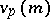 for
for 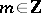 is the exponent of the largest power of the prime number
is the exponent of the largest power of the prime number 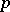 that divides
that divides 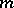 ;
; 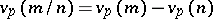 ). Now consider all formal power series
). Now consider all formal power series 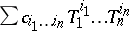 over
over 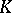 such that there exists positive numbers
such that there exists positive numbers  and
and  such that
such that 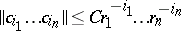 . These form a subring of
. These form a subring of 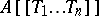 , called the ring of convergent power series over
, called the ring of convergent power series over 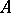 and denoted by
and denoted by 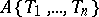 (or
(or 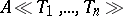 , but the latter notation also occurs for the ring of power series in non-commuting variables over
, but the latter notation also occurs for the ring of power series in non-commuting variables over  ). The Weierstrass preparation theorem also holds in
). The Weierstrass preparation theorem also holds in 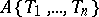 .
.
References
| [a1] | J. Berstel (ed.) , Series formelles en variables noncommutatives et aplications , Lab. Inform. Théor. Programmation (1978) |
| [a2] | M. Nagata, "Local rings" , Interscience (1960) |
Formal power series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Formal_power_series&oldid=18797