Floquet exponents
Exponents arising in the study of solutions of a linear ordinary differential equation invariant with respect to a discrete Abelian group (cf. also Floquet theory). The simplest example is a periodic ordinary differential equation
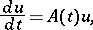 |
where  is a vector function on
is a vector function on 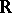 with values in a finite-dimensional complex vector space
with values in a finite-dimensional complex vector space 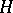 and
and 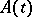 is an
is an 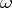 -periodic function with values in the space of linear operators in
-periodic function with values in the space of linear operators in 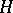 . The space of solutions of this equation is finite-dimensional and invariant with respect to the action
. The space of solutions of this equation is finite-dimensional and invariant with respect to the action 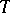 of the integer group
of the integer group 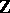 by shifts
by shifts
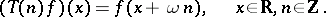 |
Here,  is the monodromy operator. One can expand any solution into eigenvectors and generalized eigenvectors of
is the monodromy operator. One can expand any solution into eigenvectors and generalized eigenvectors of  (cf. also Eigen vector). This amounts to expanding the action of
(cf. also Eigen vector). This amounts to expanding the action of 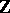 on the solution space into irreducible and primary representations (cf. also Representation of a group). If
on the solution space into irreducible and primary representations (cf. also Representation of a group). If 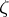 is an eigen value of
is an eigen value of 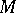 and
and 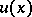 is the corresponding eigenvector, then
is the corresponding eigenvector, then
 |
The number 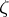 is the Floquet multiplier of
is the Floquet multiplier of  . Since
. Since  ,
, 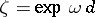 , where
, where  is the Floquet exponent. The solution (called the Floquet solution, or the Bloch solution in physics) can be represented as
is the Floquet exponent. The solution (called the Floquet solution, or the Bloch solution in physics) can be represented as
 |
with an 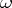 -periodic function
-periodic function 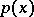 . The generalized eigenvectors can be written as
. The generalized eigenvectors can be written as
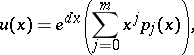 |
with an 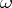 -periodic
-periodic  . Floquet solutions play a major role in any considerations involving periodic ordinary differential equations, similar to exponential-polynomial solutions in the constant-coefficient case. This approach to periodic ordinary differential equations was developed by G. Floquet [a4]. One can find detailed description and applications of this theory in many places, for instance in [a3] and [a7].
. Floquet solutions play a major role in any considerations involving periodic ordinary differential equations, similar to exponential-polynomial solutions in the constant-coefficient case. This approach to periodic ordinary differential equations was developed by G. Floquet [a4]. One can find detailed description and applications of this theory in many places, for instance in [a3] and [a7].
The Floquet theory can, to some extent, be carried over to the case of evolution equations in infinite-dimensional spaces with bounded or unbounded operator coefficient 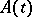 (for instance, for the time-periodic heat equation; cf. also Heat equation). One can find discussion of this matter in [a5] and [a2].
(for instance, for the time-periodic heat equation; cf. also Heat equation). One can find discussion of this matter in [a5] and [a2].
Consider now the case of a partial differential equation periodic with respect to several variables. Among the most important examples arising in applications is the Schrödinger equation 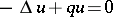 in
in 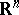 with a potential
with a potential 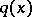 that is periodic with respect to a lattice
that is periodic with respect to a lattice 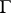 in
in 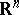 [a1]. A Floquet solution has the form
[a1]. A Floquet solution has the form 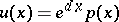 , where the Floquet exponent
, where the Floquet exponent 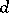 is a vector and the function
is a vector and the function 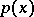 is
is 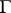 -periodic. One should note that in physics the vector
-periodic. One should note that in physics the vector 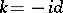 is called the quasi-momentum [a1]. Transfer of Floquet theory to the case of spatially periodic partial differential equations is possible, but non-trivial. For instance, one cannot use the monodromy operator (see [a3] and [a6] for the Schrödinger case and [a5] for more general considerations).
is called the quasi-momentum [a1]. Transfer of Floquet theory to the case of spatially periodic partial differential equations is possible, but non-trivial. For instance, one cannot use the monodromy operator (see [a3] and [a6] for the Schrödinger case and [a5] for more general considerations).
In some cases an equation can be periodic with respect to an Abelian group whose action is not just translation. Consider the magnetic Schrödinger operator
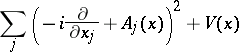 |
and define the differential form 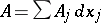 . Assume that the electric potential
. Assume that the electric potential  and the magnetic field
and the magnetic field 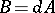 are periodic with respect to a lattice
are periodic with respect to a lattice 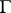 . This does not guarantee periodicity of the equation itself. However, if one combines shifts by elements of
. This does not guarantee periodicity of the equation itself. However, if one combines shifts by elements of 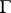 with appropriate phase shifts, one gets a discrete group (cf. also Discrete subgroup) with respect to which the equation is invariant. This group is non-commutative in general [a8], so the standard Floquet theory does not apply. However, under a rationality condition, the group is commutative and a version of magnetic Floquet theory is applicable [a8].
with appropriate phase shifts, one gets a discrete group (cf. also Discrete subgroup) with respect to which the equation is invariant. This group is non-commutative in general [a8], so the standard Floquet theory does not apply. However, under a rationality condition, the group is commutative and a version of magnetic Floquet theory is applicable [a8].
References
| [a1] | N.W. Ashcroft, N.D. Mermin, "Solid State Physics" , Holt, Rinehart&Winston (1976) |
| [a2] | Ju.L. Daleckii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Transl. Math. Monogr. , 43 , Amer. Math. Soc. (1974) |
| [a3] | M.S.P. Eastham, "The spectral theory of periodic differential equations" , Scottish Acad. Press (1973) |
| [a4] | G. Floquet, "Sur les equations differentielles lineaires a coefficients periodique" Ann. Ecole Norm. Ser. 2 , 12 (1883) pp. 47–89 |
| [a5] | P. Kuchment, "Floquet theory for partial differential equations" , Birkhäuser (1993) |
| [a6] | M. Reed, B. Simon, "Methods of modern mathematical physics: Analysis of operators" , IV , Acad. Press (1978) |
| [a7] | V.A. Yakubovich, V.M. Starzhinskii, "Linear differential equations with periodic coefficients" , 1, 2 , Halsted Press&Wiley (1975) |
| [a8] | J. Zak, "Magnetic translation group" Phys. Rev. , 134 (1964) pp. A1602–A1611 |
Floquet exponents. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Floquet_exponents&oldid=14228