Floor function
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
entier function, greatest integer function, integral part function
The function of a real variable that assigns to a real number  the largest integer
the largest integer 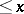 . The modern notation is
. The modern notation is 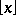 ; the classical notation is
; the classical notation is 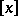 . In computer science and computer languages it is often denoted by
. In computer science and computer languages it is often denoted by 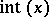 .
.
The related ceiling function  gives the smallest integer
gives the smallest integer 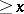 . The fractional part function is defined as
. The fractional part function is defined as
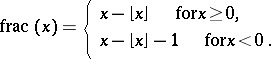 |
The nearest integer function is
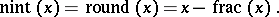 |
References
| [a1] | R.L. Graham, D.E. Knuth, O. Patashnik, "Concrete mathematics: a foundation for computer science" , Addison-Wesley (1990) |
| [a2] | S. Wolfram, "Mathematica: Version 3" , Addison-Wesley (1996) pp. 718–719 |
How to Cite This Entry:
Floor function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Floor_function&oldid=17649
Floor function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Floor_function&oldid=17649
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article