Floor function
From Encyclopedia of Mathematics
entier function, greatest integer function, integral part function
The function of a real variable that assigns to a real number 
the largest integer 
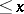. The modern notation is 
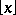; the classical notation is 
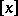. In computer science and computer languages it is often denoted by 
.
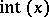The related ceiling function 
gives the smallest integer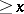 
. The fractional part function is defined as
 |
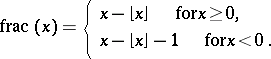The nearest integer function is
 |
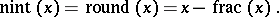References
| [a1] | R.L. Graham, D.E. Knuth, O. Patashnik, "Concrete mathematics: a foundation for computer science" , Addison-Wesley (1990) |
| [a2] | S. Wolfram, "Mathematica: Version 3" , Addison-Wesley (1996) pp. 718–719 |
How to Cite This Entry:
Floor function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Floor_function&oldid=17649
Floor function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Floor_function&oldid=17649
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article