Flecnode
From Encyclopedia of Mathematics
on a planar curve
A point at which a node (or double point; cf. also Node) and an inflection (cf. also Point of inflection) coincide.
Thus, one of the tangents at the node has intersection multiplicity at least 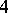 with the curve at that point.
with the curve at that point.
References
| [a1] | J.W. Bruce, "Lines, surfaces and duality" Math. Proc. Cambridge Philos. Soc. , 112 (1992) pp. 53–61 |
| [a2] | M. Tsuboko, "On the line complex determinant of flecnode tangents of a ruled surface and its flecnodal surfaces" Memoirs Ryojun Coll. Engin. , 11 (1938) pp. 233–238 |
How to Cite This Entry:
Flecnode. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flecnode&oldid=18929
Flecnode. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flecnode&oldid=18929
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article