Flat morphism
A morphism of schemes 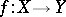 such that for any point
such that for any point 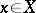 the local ring
the local ring  is flat over
is flat over  (see Flat module). In general, let
(see Flat module). In general, let 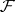 be a sheaf of
be a sheaf of 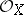 -modules; it is called flat over
-modules; it is called flat over 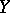 at a point
at a point 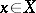 if
if 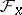 is a flat module over the ring
is a flat module over the ring 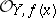 . Subject to certain (fairly weak) finiteness conditions, the set of points at which a coherent
. Subject to certain (fairly weak) finiteness conditions, the set of points at which a coherent 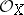 -module
-module 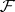 is flat over
is flat over 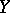 is open in
is open in 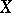 . If, moreover,
. If, moreover, 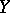 is an integral scheme, then there exists an open non-empty subset
is an integral scheme, then there exists an open non-empty subset 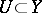 such that
such that 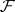 is a flat sheaf over
is a flat sheaf over 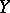 at all points lying above
at all points lying above 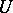 .
.
A flat morphism of finite type corresponds to the intuitive concept of a continuous family of varieties. A flat morphism is open and equi-dimensional (i.e. the dimensions of the fibres 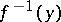 are locally constant for
are locally constant for 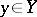 ). For many geometric properties, the set of points
). For many geometric properties, the set of points  at which the fibre
at which the fibre 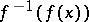 of a flat morphism
of a flat morphism 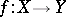 has this property is open in
has this property is open in 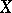 . If a flat morphism
. If a flat morphism 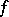 is proper (cf. Proper morphism), then the set of points
is proper (cf. Proper morphism), then the set of points 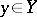 for which the fibres over them have this property is open .
for which the fibres over them have this property is open .
Flat morphisms are used also in descent theory. A morphism of schemes is called faithfully flat if it is flat and surjective. Then, as a rule, one may check any property of a certain object over 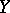 simply by checking this property for the object obtained after a faithfully-flat base change
simply by checking this property for the object obtained after a faithfully-flat base change 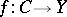 . In this connection, interest attaches to flatness criteria for a morphism
. In this connection, interest attaches to flatness criteria for a morphism 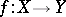 (or for the
(or for the  -module
-module 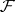 ); here
); here 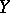 can be regarded as a local scheme. The simplest criterion relates to the case where the base
can be regarded as a local scheme. The simplest criterion relates to the case where the base  is one-dimensional and regular: A coherent
is one-dimensional and regular: A coherent  -module
-module 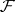 is flat if and only if the uniformizing parameter in
is flat if and only if the uniformizing parameter in 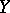 has a trivial annihilator in
has a trivial annihilator in 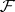 . In a certain sense the general case is reducible to the one-dimensional case. Let
. In a certain sense the general case is reducible to the one-dimensional case. Let 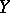 be a reduced Noetherian scheme and let for any morphism
be a reduced Noetherian scheme and let for any morphism 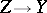 , where
, where 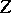 is a one-dimensional regular scheme, the base change
is a one-dimensional regular scheme, the base change 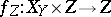 be a flat morphism; then
be a flat morphism; then  is a flat morphism. Another flatness criterion requires that
is a flat morphism. Another flatness criterion requires that  is universally open, while
is universally open, while 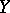 and the geometric fibres
and the geometric fibres 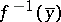 are reduced.
are reduced.
References
| [1a] | A. Grothendieck, J. Dieudonné, "Eléments de géométrie algébrique" Publ. Math. IHES , 24 (1964) |
| [1b] | A. Grothendieck, J. Dieudonné, "Eléments de géométrie algébrique" Publ. Math. IHES , 28 (1966) |
| [2] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) |
| [3] | M. Raynaud, L. Gruson, "Critères de platitude et de projectivité. Techniques de "platification" d'un module" Invent. Math. , 13 (1971) pp. 1–89 |
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Flat morphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flat_morphism&oldid=12305