Flat module
A left (or right) module  over an associative ring
over an associative ring  such that the tensor-product functor
such that the tensor-product functor  (correspondingly,
(correspondingly,  ) is exact. This definition is equivalent to any of the following: 1) the functor
) is exact. This definition is equivalent to any of the following: 1) the functor  (correspondingly,
(correspondingly,  ); 2) the module
); 2) the module  can be represented in the form of a direct (injective) limit of summands of free modules; 3) the character module
can be represented in the form of a direct (injective) limit of summands of free modules; 3) the character module  is injective, where
is injective, where 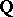 is the group of rational numbers and
is the group of rational numbers and 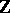 is the group of integers; and 4) for any right (correspondingly, left) ideal
is the group of integers; and 4) for any right (correspondingly, left) ideal 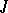 of
of 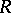 , the canonical homomorphism
, the canonical homomorphism
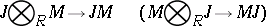 |
is an isomorphism.
Projective modules and free modules are examples of flat modules (cf. Projective module; Free module). The class of flat modules over the ring of integers coincides with the class of Abelian groups without torsion. All modules over a ring  are flat modules if and only if
are flat modules if and only if 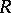 is regular in the sense of von Neumann (see Absolutely-flat ring). A coherent ring
is regular in the sense of von Neumann (see Absolutely-flat ring). A coherent ring 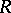 can be defined as a ring over which the direct product
can be defined as a ring over which the direct product 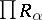 of any number of copies of
of any number of copies of 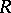 is a flat module. The operations of localization and completion with respect to powers of an ideal of a ring
is a flat module. The operations of localization and completion with respect to powers of an ideal of a ring 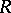 lead to flat modules over the ring (see Adic topology). The classical ring of fractions of a ring
lead to flat modules over the ring (see Adic topology). The classical ring of fractions of a ring 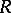 is a flat module over
is a flat module over 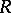 .
.
References
| [1] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [2] | J. Lambek, "Lectures on rings and modules" , Blaisdell (1966) |
Comments
References
| [a1] | N. Bourbaki, "Commutative algebra" , Addison-Wesley (1964) (Translated from French) |
Flat module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flat_module&oldid=17725