Flag structure
The same as a flag.
A flag structure of type 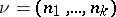 on an
on an  -dimensional manifold
-dimensional manifold 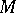 is a field of flags
is a field of flags 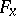 of type
of type  defined by subspaces
defined by subspaces
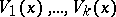 |
of the tangent spaces 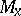 , depending smoothly on the point
, depending smoothly on the point  . In other words, a flag structure of type
. In other words, a flag structure of type  on
on 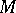 is a smooth section of the bundle of flags of type
is a smooth section of the bundle of flags of type  on
on 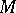 , the typical fibre of which at the point
, the typical fibre of which at the point 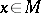 is the variety
is the variety 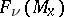 . A flag structure of type
. A flag structure of type 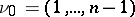 is called complete or full. A flag structure of type
is called complete or full. A flag structure of type  on a manifold is a
on a manifold is a 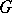 -structure, where
-structure, where 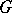 is the group of all linear transformations of the
is the group of all linear transformations of the  -dimensional vector space preserving some flag of type
-dimensional vector space preserving some flag of type  . This
. This 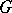 -structure is of infinite type. The automorphism group of a flag structure is, generally speaking, infinite-dimensional. The Lie algebra
-structure is of infinite type. The automorphism group of a flag structure is, generally speaking, infinite-dimensional. The Lie algebra 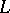 of infinitesimal automorphisms of a flag structure on
of infinitesimal automorphisms of a flag structure on 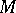 has a chain of ideals
has a chain of ideals 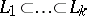 , where
, where 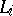 consists of the vector fields
consists of the vector fields 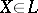 such that
such that 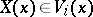 for all
for all  .
.
An important special case of flag structures are those of type 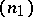 , or
, or 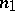 -dimensional distributions (here
-dimensional distributions (here 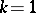 ,
,  ).
).
A flag structure of type  on
on 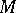 is called locally flat, or integrable, if every point
is called locally flat, or integrable, if every point 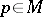 has a neighbourhood
has a neighbourhood 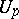 and a coordinate system
and a coordinate system 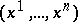 in it such that the subspace
in it such that the subspace 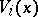 is spanned by the vectors
is spanned by the vectors
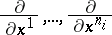 |
for all 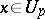 and all
and all 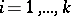 . This means that
. This means that 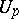 has a collection of foliations
has a collection of foliations 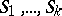 such that for all
such that for all 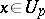 the flag
the flag 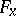 is defined by a collection of subspaces of
is defined by a collection of subspaces of 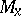 tangent to the leaves of these foliations passing through
tangent to the leaves of these foliations passing through  . A flag structure is locally flat if and only if for every
. A flag structure is locally flat if and only if for every 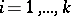 the distribution
the distribution 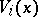 is involutory, that is, if for any two vector fields
is involutory, that is, if for any two vector fields 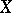 and
and 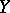 on
on 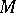 such that
such that 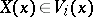 and
and 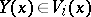 for all
for all 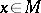 , it is true that
, it is true that
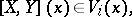 |
where 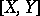 is the Lie bracket of
is the Lie bracket of  and
and 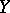 .
.
The existence of global (everywhere-defined) flag structures on a manifold imposes fairly-strong restrictions on its topological structure. For example, there is a line field, that is, a flag structure of type , on a simply-connected compact manifold if and only if its Euler characteristic vanishes. There is a complete flag structure on a simply-connected manifold if and only if it is completely parallelizable, that is, if its tangent bundle is trivial. If there is a parallel flag structure of type 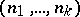 that is invariant relative to parallel displacements on a complete simply-connected
that is invariant relative to parallel displacements on a complete simply-connected  -dimensional Riemannian manifold
-dimensional Riemannian manifold 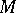 , then
, then 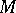 is isomorphic to the direct product of simply-connected Riemannian manifolds of dimensions
is isomorphic to the direct product of simply-connected Riemannian manifolds of dimensions
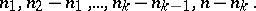 |
A transitive group of diffeomorphisms of a manifold 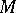 leaves some flag structure of type
leaves some flag structure of type  on
on 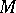 invariant if and only if its linear isotropy group preserves some flag of type
invariant if and only if its linear isotropy group preserves some flag of type  in the tangent space to
in the tangent space to  . In particular, if
. In particular, if 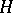 is a closed subgroup of a Lie group
is a closed subgroup of a Lie group 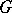 such that the restriction to
such that the restriction to 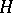 of the adjoint representation of
of the adjoint representation of 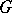 gives a triangular linear group, then there is an invariant complete flag structure on the homogeneous space
gives a triangular linear group, then there is an invariant complete flag structure on the homogeneous space 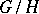 , and also an invariant flag structure of every other type.
, and also an invariant flag structure of every other type.
A theory of deformations of flag structures on compact manifolds has been developed [4].
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) |
| [3] | I.N. Bernshtein, I.M. Gel'fand, S.I. Gel'fand, "Schubert cells and cohomology of the spaces 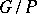 " Russian Math. Surveys , 28 : 3 (1973) pp. 1–26 Uspekhi Mat. Nauk , 28 : 3 (1973) pp. 3–26 " Russian Math. Surveys , 28 : 3 (1973) pp. 1–26 Uspekhi Mat. Nauk , 28 : 3 (1973) pp. 3–26 |
| [4] | K. Kodaira, D.C. Spencer, "Multifoliate structures" Ann. of Math. , 74 (1961) pp. 52–100 |
Flag structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flag_structure&oldid=17937