Flag space
A projective  -space whose metric is defined by an absolute consisting of a collection of
-space whose metric is defined by an absolute consisting of a collection of 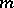 -planes,
-planes, 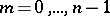 , imbedded in one another, called a flag; a flag space is denoted by
, imbedded in one another, called a flag; a flag space is denoted by 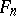 . The absolute of a flag space can be obtained from the absolutes of Galilean or pseudo-Galilean spaces by means of a passing to the limit in the quadrics of the absolutes. In particular, the flag (absolute) of the space
. The absolute of a flag space can be obtained from the absolutes of Galilean or pseudo-Galilean spaces by means of a passing to the limit in the quadrics of the absolutes. In particular, the flag (absolute) of the space 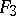 consists of a
consists of a  -plane
-plane 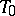 , in which lies a line
, in which lies a line 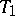 (a Euclidean line), and on the line a point
(a Euclidean line), and on the line a point 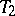 . The plane
. The plane 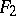 is a projective
is a projective  -plane with a distinguished line
-plane with a distinguished line 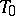 and a distinguished point
and a distinguished point 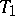 and coincides with Yaglom's Galilean plane.
and coincides with Yaglom's Galilean plane. 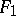 is a projective line with a distinguished point
is a projective line with a distinguished point 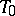 , and is the same as the Euclidean line.
, and is the same as the Euclidean line.
If one chooses an affine coordinate system  in a flag space
in a flag space 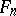 so that the vectors of the lines passing through the
so that the vectors of the lines passing through the 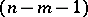 -plane
-plane 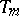 are defined by the condition
are defined by the condition 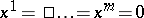 , then one takes the number
, then one takes the number 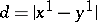 as the distance between the points
as the distance between the points 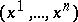 and
and 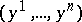 ; if
; if 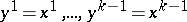 , then the distance is defined by the number
, then the distance is defined by the number 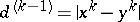 .
.
Lines that intersect the 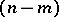 -plane and not the
-plane and not the 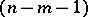 -plane are called lines of order
-plane are called lines of order 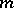 .
.
Motions of a flag space are collineations mapping the absolute into itself. The motions of a flag space form a subgroup of the affine transformations of an affine  -space, and this group of motions of a flag space is a Lie group.
-space, and this group of motions of a flag space is a Lie group.
A space 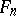 is self-dual. As the value of the angle between two
is self-dual. As the value of the angle between two 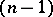 -planes one takes the distance between the points dual to these planes.
-planes one takes the distance between the points dual to these planes.
A flag space is a special case of a semi-elliptic space. In particular, the flag space 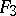 is the same as the
is the same as the  -space
-space 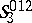 . The flag
. The flag  -space is the unique space with parabolic distance metrics on lines, in semi-planes and in bundles of planes.
-space is the unique space with parabolic distance metrics on lines, in semi-planes and in bundles of planes.
References
| [1] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
Comments
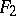 , or Yaglom's Galilean plane, may be described as follows. Recall Poncelet's description of the Euclidean plane as a projective plane with a metric determined by two "circular points"
, or Yaglom's Galilean plane, may be described as follows. Recall Poncelet's description of the Euclidean plane as a projective plane with a metric determined by two "circular points" 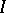 and
and 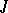 whose join
whose join  is the line at infinity. I.M. Yaglom considered a modification in which
is the line at infinity. I.M. Yaglom considered a modification in which 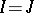 while
while  is still a special line through
is still a special line through 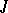 . In other words, the new metric is determined by the flag
. In other words, the new metric is determined by the flag 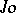 . The role of circles, which were conics (cf. Cone) through
. The role of circles, which were conics (cf. Cone) through 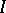 and
and 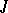 , is taken over by conics touching
, is taken over by conics touching  at
at 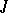 , i.e. by parabolas whose diameters all have the same direction (cf. Parabola). Lines in that direction (through
, i.e. by parabolas whose diameters all have the same direction (cf. Parabola). Lines in that direction (through 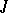 ) behave differently from other lines. In general,
) behave differently from other lines. In general, 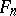 contains lines of
contains lines of  distinct types.
distinct types.
For absolute of a space see Absolute; see also Galilean space; Pseudo-Galilean space.
References
| [a1] | H.S.M. Coxeter, "The affine aspect of Yaglom's Galilean Feuerbach" Nieuw Archief voor Wiskunde (4) , 1 (1983) pp. 212–223 |
| [a2] | I.M. Yaglom, "A simple non-Euclidean geometry and its physical basis" , Springer (1979) (Translated from Russian) |
Flag space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flag_space&oldid=14163