Flag
of type  in an
in an  -dimensional vector space
-dimensional vector space 
A collection of linear subspaces 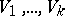 of
of  of corresponding dimensions
of corresponding dimensions  , such that
, such that 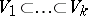 (here
(here  ,
, 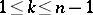 ;
; 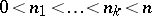 ). A flag of type
). A flag of type 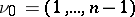 is called a complete flag or a full flag. Any two flags of the same type can be mapped to each other by some linear transformation of
is called a complete flag or a full flag. Any two flags of the same type can be mapped to each other by some linear transformation of 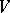 , that is, the set
, that is, the set 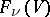 of all flags of type
of all flags of type  in
in 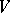 is a homogeneous space of the general linear group
is a homogeneous space of the general linear group 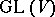 . The unimodular group
. The unimodular group 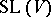 also acts transitively on
also acts transitively on 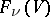 . Here the stationary subgroup
. Here the stationary subgroup 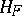 of
of  in
in 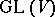 (and also in
(and also in 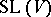 ) is a parabolic subgroup of
) is a parabolic subgroup of 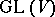 (respectively, of
(respectively, of 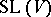 ). If
). If 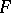 is a complete flag in
is a complete flag in 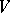 , defined by subspaces
, defined by subspaces  , then
, then 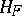 is a complete triangular subgroup of
is a complete triangular subgroup of 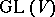 (respectively, of
(respectively, of 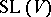 ) relative to a basis
) relative to a basis  of
of 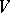 such that
such that 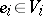 ,
, 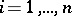 . In general, quotient spaces of linear algebraic groups by parabolic subgroups are sometimes called flag varieties. For
. In general, quotient spaces of linear algebraic groups by parabolic subgroups are sometimes called flag varieties. For 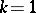 , a flag of type
, a flag of type  is simply an
is simply an 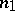 -dimensional linear subspace of
-dimensional linear subspace of 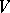 and
and 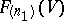 is the Grassmann manifold
is the Grassmann manifold 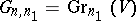 . In particular,
. In particular, 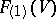 is the projective space associated with the vector space
is the projective space associated with the vector space 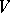 . Every flag variety
. Every flag variety 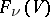 can be canonically equipped with the structure of a projective algebraic variety (see ). If
can be canonically equipped with the structure of a projective algebraic variety (see ). If 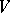 is a real or complex vector space, then all the varieties
is a real or complex vector space, then all the varieties 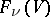 are compact. Cellular decompositions and cohomology rings of the
are compact. Cellular decompositions and cohomology rings of the 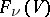 are known (see , and also Bruhat decomposition).
are known (see , and also Bruhat decomposition).
For references see Flag structure.
Flag. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flag&oldid=19141