Difference between revisions of "Flag"
(Importing text file) |
(restore reference numbers from printed version) |
||
| Line 1: | Line 1: | ||
''of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405502.png" /> in an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405503.png" />-dimensional vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405504.png" />'' | ''of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405502.png" /> in an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405503.png" />-dimensional vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405504.png" />'' | ||
| − | A collection of linear subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405505.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405506.png" /> of corresponding dimensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405507.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405508.png" /> (here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405509.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055010.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055011.png" />). A flag of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055012.png" /> is called a complete flag or a full flag. Any two flags of the same type can be mapped to each other by some linear transformation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055013.png" />, that is, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055014.png" /> of all flags of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055015.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055016.png" /> is a homogeneous space of the general linear group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055017.png" />. The unimodular group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055018.png" /> also acts transitively on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055019.png" />. Here the stationary subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055020.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055021.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055022.png" /> (and also in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055023.png" />) is a parabolic subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055024.png" /> (respectively, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055025.png" />). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055026.png" /> is a complete flag in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055027.png" />, defined by subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055028.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055029.png" /> is a complete triangular subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055030.png" /> (respectively, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055031.png" />) relative to a basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055032.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055033.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055034.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055035.png" />. In general, quotient spaces of linear algebraic groups by parabolic subgroups are sometimes called flag varieties. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055036.png" />, a flag of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055037.png" /> is simply an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055038.png" />-dimensional linear subspace of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055039.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055040.png" /> is the [[Grassmann manifold|Grassmann manifold]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055041.png" />. In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055042.png" /> is the projective space associated with the vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055043.png" />. Every flag variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055044.png" /> can be canonically equipped with the structure of a projective algebraic variety (see ). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055045.png" /> is a real or complex vector space, then all the varieties <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055046.png" /> are compact. Cellular decompositions and cohomology rings of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055047.png" /> are known (see , and also [[Bruhat decomposition|Bruhat decomposition]]). | + | A collection of linear subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405505.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405506.png" /> of corresponding dimensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405507.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405508.png" /> (here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f0405509.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055010.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055011.png" />). A flag of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055012.png" /> is called a complete flag or a full flag. Any two flags of the same type can be mapped to each other by some linear transformation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055013.png" />, that is, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055014.png" /> of all flags of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055015.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055016.png" /> is a homogeneous space of the general linear group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055017.png" />. The unimodular group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055018.png" /> also acts transitively on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055019.png" />. Here the stationary subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055020.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055021.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055022.png" /> (and also in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055023.png" />) is a parabolic subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055024.png" /> (respectively, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055025.png" />). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055026.png" /> is a complete flag in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055027.png" />, defined by subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055028.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055029.png" /> is a complete triangular subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055030.png" /> (respectively, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055031.png" />) relative to a basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055032.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055033.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055034.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055035.png" />. In general, quotient spaces of linear algebraic groups by parabolic subgroups are sometimes called flag varieties. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055036.png" />, a flag of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055037.png" /> is simply an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055038.png" />-dimensional linear subspace of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055039.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055040.png" /> is the [[Grassmann manifold|Grassmann manifold]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055041.png" />. In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055042.png" /> is the projective space associated with the vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055043.png" />. Every flag variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055044.png" /> can be canonically equipped with the structure of a projective algebraic variety (see [1]). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055045.png" /> is a real or complex vector space, then all the varieties <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055046.png" /> are compact. Cellular decompositions and cohomology rings of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040550/f04055047.png" /> are known (see [3], and also [[Bruhat decomposition|Bruhat decomposition]]). |
For references see [[Flag structure|Flag structure]]. | For references see [[Flag structure|Flag structure]]. | ||
Revision as of 08:29, 10 April 2018
of type  in an
in an  -dimensional vector space
-dimensional vector space 
A collection of linear subspaces 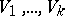 of
of  of corresponding dimensions
of corresponding dimensions  , such that
, such that 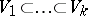 (here
(here  ,
, 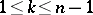 ;
; 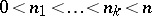 ). A flag of type
). A flag of type 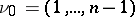 is called a complete flag or a full flag. Any two flags of the same type can be mapped to each other by some linear transformation of
is called a complete flag or a full flag. Any two flags of the same type can be mapped to each other by some linear transformation of 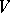 , that is, the set
, that is, the set 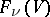 of all flags of type
of all flags of type  in
in 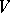 is a homogeneous space of the general linear group
is a homogeneous space of the general linear group 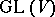 . The unimodular group
. The unimodular group 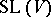 also acts transitively on
also acts transitively on 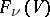 . Here the stationary subgroup
. Here the stationary subgroup 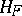 of
of  in
in 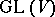 (and also in
(and also in 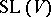 ) is a parabolic subgroup of
) is a parabolic subgroup of 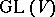 (respectively, of
(respectively, of 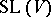 ). If
). If 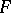 is a complete flag in
is a complete flag in 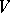 , defined by subspaces
, defined by subspaces  , then
, then 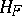 is a complete triangular subgroup of
is a complete triangular subgroup of 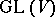 (respectively, of
(respectively, of 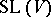 ) relative to a basis
) relative to a basis  of
of 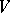 such that
such that 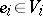 ,
, 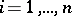 . In general, quotient spaces of linear algebraic groups by parabolic subgroups are sometimes called flag varieties. For
. In general, quotient spaces of linear algebraic groups by parabolic subgroups are sometimes called flag varieties. For 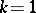 , a flag of type
, a flag of type  is simply an
is simply an 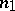 -dimensional linear subspace of
-dimensional linear subspace of 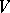 and
and 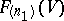 is the Grassmann manifold
is the Grassmann manifold 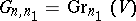 . In particular,
. In particular, 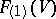 is the projective space associated with the vector space
is the projective space associated with the vector space 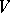 . Every flag variety
. Every flag variety 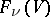 can be canonically equipped with the structure of a projective algebraic variety (see [1]). If
can be canonically equipped with the structure of a projective algebraic variety (see [1]). If 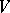 is a real or complex vector space, then all the varieties
is a real or complex vector space, then all the varieties 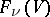 are compact. Cellular decompositions and cohomology rings of the
are compact. Cellular decompositions and cohomology rings of the 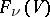 are known (see [3], and also Bruhat decomposition).
are known (see [3], and also Bruhat decomposition).
For references see Flag structure.
Flag. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flag&oldid=19141