Fitting subgroup
The characteristic subgroup 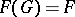 of a group
of a group 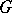 generated by all the nilpotent normal subgroups of
generated by all the nilpotent normal subgroups of 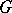 ; it is also called the Fitting radical. It was first studied by H. Fitting [1]. For finite groups, the Fitting subgroup is nilpotent and is the unique maximal nilpotent normal subgroup of the group. For a finite group
; it is also called the Fitting radical. It was first studied by H. Fitting [1]. For finite groups, the Fitting subgroup is nilpotent and is the unique maximal nilpotent normal subgroup of the group. For a finite group 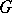 the following relations hold:
the following relations hold:
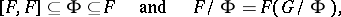 |
where 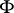 denotes the Frattini subgroup of
denotes the Frattini subgroup of 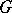 , and
, and  is the commutator subgroup of
is the commutator subgroup of 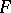 .
.
References
| [1] | H. Fitting, "Beiträge zur Theorie der Gruppen endlicher Ordnung" Jahresber. Deutsch. Math.-Verein , 48 (1938) pp. 77–141 |
| [2] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [3] | D. Gorenstein, "Finite groups" , Harper & Row (1968) |
Comments
A finite group 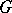 is called quasi-nilpotent if and only if for every chief factor
is called quasi-nilpotent if and only if for every chief factor 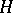 of
of 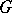 every automorphism of
every automorphism of 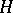 induced by an element of
induced by an element of 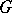 is inner. Let
is inner. Let 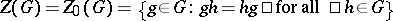 be the centre of
be the centre of 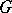 . Inductively define
. Inductively define 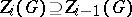 ,
, 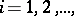 by the condition
by the condition 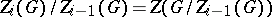 . The
. The 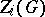 are all normal subgroups. The series
are all normal subgroups. The series 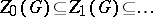 is the ascending central series of
is the ascending central series of 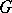 . Let
. Let 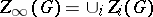 , the so-called hypercentre of
, the so-called hypercentre of 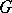 . A group
. A group 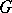 is semi-simple if and only if it is the direct product of non-Abelian simple groups. A group
is semi-simple if and only if it is the direct product of non-Abelian simple groups. A group 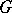 is quasi-nilpotent if and only if
is quasi-nilpotent if and only if 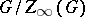 is semi-simple. The generalized Fitting subgroup of a finite group
is semi-simple. The generalized Fitting subgroup of a finite group 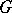 is the set of all elements
is the set of all elements  of
of 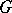 which induce an inner automorphism on every chief factor of
which induce an inner automorphism on every chief factor of 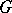 . It is a characteristic subgroup of
. It is a characteristic subgroup of 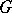 and contains every subnormal quasi-nilpotent subgroup of
and contains every subnormal quasi-nilpotent subgroup of  . This property can therefore also be used to define it.
. This property can therefore also be used to define it.
Let 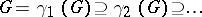 be the lower central series of
be the lower central series of 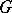 , i.e.
, i.e. 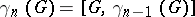 , the commutator subgroup of
, the commutator subgroup of 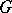 with
with 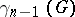 . Let
. Let 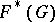 be the generalized Fitting subgroup of
be the generalized Fitting subgroup of 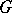 ; then
; then 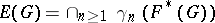 is a perfect quasi-nilpotent characteristic subgroup. It is sometimes called the layer of
is a perfect quasi-nilpotent characteristic subgroup. It is sometimes called the layer of  .
.
References
| [a1] | B. Huppert, "Endliche Gruppen" , 1 , Springer (1967) |
| [a2] | B. Huppert, "Finite groups" , 2–3 , Springer (1982) |
| [a3] | D.J.S. Robinson, "A course in the theory of groups" , Springer (1982) |
Fitting subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fitting_subgroup&oldid=17227