Difference between revisions of "Finite group scheme"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | f0402901.png | ||
| + | $#A+1 = 51 n = 3 | ||
| + | $#C+1 = 51 : ~/encyclopedia/old_files/data/F040/F.0400290 Finite group scheme | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | If | + | {{TEX|auto}} |
| + | {{TEX|done}} | ||
| + | |||
| + | A group scheme that is finite and flat over the ground scheme. If $ G $ | ||
| + | is a finite group scheme over a scheme $ ( G, {\mathcal O} _ {S} ) $, | ||
| + | then $ G = \mathop{\rm Spec} {\mathcal A} $, | ||
| + | where $ {\mathcal A} $ | ||
| + | is a finite flat quasi-coherent sheaf of algebras over $ {\mathcal O} _ {S} $. | ||
| + | From now on it is assumed that $ S $ | ||
| + | is locally Noetherian. In this case $ {\mathcal A} $ | ||
| + | is locally free. If $ S $ | ||
| + | is connected, then the rank of $ {\mathcal A} \times _ { {\mathcal O} _ {s} } k ( s) $ | ||
| + | over the field of residues $ k ( s) $ | ||
| + | at a point $ s \in S $ | ||
| + | is independent of $ s $ | ||
| + | and is called the rank of the finite group scheme. Let $ n _ {G} : G \rightarrow G $ | ||
| + | be the morphism of $ S $- | ||
| + | schemes mapping an element $ s \in G ( T) $ | ||
| + | into $ x ^ {n} \in G ( T) $, | ||
| + | where $ T $ | ||
| + | is an arbitrary $ S $- | ||
| + | scheme. The morphism $ n _ {G} $ | ||
| + | is null if the rank of $ G $ | ||
| + | divides $ n $ | ||
| + | and if $ S $ | ||
| + | is a reduced scheme or if $ G $ | ||
| + | is a commutative finite group scheme (see [[Commutative group scheme|Commutative group scheme]]). Every finite group scheme of rank $ p $, | ||
| + | where $ p $ | ||
| + | is a prime number, is commutative [[#References|[2]]]. | ||
| + | |||
| + | If $ G _ {1} $ | ||
| + | is a subgroup of a finite group scheme $ G $, | ||
| + | then one can form the finite group scheme $ G/G _ {1} $, | ||
| + | and the rank of $ G $ | ||
| + | is the product of the ranks of $ G _ {1} $ | ||
| + | and $ G/G _ {1} $. | ||
===Examples.=== | ===Examples.=== | ||
| + | 1) Let $ G = G _ {mS} $ | ||
| + | be a multiplicative group scheme (or Abelian scheme $ {\mathcal A} $ | ||
| + | over $ S $); | ||
| + | then $ \mathop{\rm Ker} n _ {G} $ | ||
| + | is a finite group scheme of rank $ | n | $( | ||
| + | or $ | n | ^ {2 \mathop{\rm dim} {\mathcal A} } $). | ||
| − | + | 2) Let $ S $ | |
| + | be a scheme over the prime field $ \mathbf F _ {p} $ | ||
| + | and let $ F: G _ {aS} \rightarrow G _ {aS} $ | ||
| + | be the Frobenius homomorphism of the additive group scheme $ G _ {aS} $. | ||
| + | Then $ \mathop{\rm Ker} F $ | ||
| + | is a finite group scheme of rank $ p $. | ||
| − | + | 3) For every abstract finite group scheme $ \Gamma $ | |
| + | of order $ n $ | ||
| + | the constant group scheme $ \Gamma _ {S} $ | ||
| + | is a finite group scheme of rank $ n $. | ||
| − | + | The classification of finite group schemes over arbitrary ground schemes has been achieved in the case where the rank of $ G $ | |
| − | + | is a prime number (cf. [[#References|[2]]]). The case where $ G $ | |
| − | The classification of finite group schemes over arbitrary ground schemes has been achieved in the case where the rank of | + | is a commutative finite group scheme and $ S $ |
| + | is the spectrum of a field of characteristic $ p $ | ||
| + | is well known (see [[#References|[1]]], [[#References|[3]]], [[#References|[7]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" ''Russian Math. Surveys'' , '''18''' (1963) pp. 1–80 ''Uspekhi Mat. Nauk'' , '''18''' : 6 (1963) pp. 3–90</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Tate, F. Oort, "Group schemes of prime order" ''Ann. Sci. Ecole Norm. Sup.'' , '''3''' (1970) pp. 1–21</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Demazure, P. Gabriel, "Groupes algébriques" , '''1''' , Masson (1970)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> F. Oort, "Commutative group schemes" , ''Lect. notes in math.'' , '''15''' , Springer (1966)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S. Shatz, "Cohomology of Artinian group schemes over local fields" ''Ann. of Math.'' , '''79''' (1964) pp. 411–449</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Mazur, "Notes on étale cohomology of number fields" ''Ann. Sci. Ecole Norm. Sup.'' , '''6''' (1973) pp. 521–556</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> H. Kraft, "Kommutative algebraische Gruppen und Ringe" , Springer (1975)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" ''Russian Math. Surveys'' , '''18''' (1963) pp. 1–80 ''Uspekhi Mat. Nauk'' , '''18''' : 6 (1963) pp. 3–90</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Tate, F. Oort, "Group schemes of prime order" ''Ann. Sci. Ecole Norm. Sup.'' , '''3''' (1970) pp. 1–21</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Demazure, P. Gabriel, "Groupes algébriques" , '''1''' , Masson (1970)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> F. Oort, "Commutative group schemes" , ''Lect. notes in math.'' , '''15''' , Springer (1966)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S. Shatz, "Cohomology of Artinian group schemes over local fields" ''Ann. of Math.'' , '''79''' (1964) pp. 411–449</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Mazur, "Notes on étale cohomology of number fields" ''Ann. Sci. Ecole Norm. Sup.'' , '''6''' (1973) pp. 521–556</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> H. Kraft, "Kommutative algebraische Gruppen und Ringe" , Springer (1975)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 19:39, 5 June 2020
A group scheme that is finite and flat over the ground scheme. If $ G $
is a finite group scheme over a scheme $ ( G, {\mathcal O} _ {S} ) $,
then $ G = \mathop{\rm Spec} {\mathcal A} $,
where $ {\mathcal A} $
is a finite flat quasi-coherent sheaf of algebras over $ {\mathcal O} _ {S} $.
From now on it is assumed that $ S $
is locally Noetherian. In this case $ {\mathcal A} $
is locally free. If $ S $
is connected, then the rank of $ {\mathcal A} \times _ { {\mathcal O} _ {s} } k ( s) $
over the field of residues $ k ( s) $
at a point $ s \in S $
is independent of $ s $
and is called the rank of the finite group scheme. Let $ n _ {G} : G \rightarrow G $
be the morphism of $ S $-
schemes mapping an element $ s \in G ( T) $
into $ x ^ {n} \in G ( T) $,
where $ T $
is an arbitrary $ S $-
scheme. The morphism $ n _ {G} $
is null if the rank of $ G $
divides $ n $
and if $ S $
is a reduced scheme or if $ G $
is a commutative finite group scheme (see Commutative group scheme). Every finite group scheme of rank $ p $,
where $ p $
is a prime number, is commutative [2].
If $ G _ {1} $ is a subgroup of a finite group scheme $ G $, then one can form the finite group scheme $ G/G _ {1} $, and the rank of $ G $ is the product of the ranks of $ G _ {1} $ and $ G/G _ {1} $.
Examples.
1) Let $ G = G _ {mS} $ be a multiplicative group scheme (or Abelian scheme $ {\mathcal A} $ over $ S $); then $ \mathop{\rm Ker} n _ {G} $ is a finite group scheme of rank $ | n | $( or $ | n | ^ {2 \mathop{\rm dim} {\mathcal A} } $).
2) Let $ S $ be a scheme over the prime field $ \mathbf F _ {p} $ and let $ F: G _ {aS} \rightarrow G _ {aS} $ be the Frobenius homomorphism of the additive group scheme $ G _ {aS} $. Then $ \mathop{\rm Ker} F $ is a finite group scheme of rank $ p $.
3) For every abstract finite group scheme $ \Gamma $ of order $ n $ the constant group scheme $ \Gamma _ {S} $ is a finite group scheme of rank $ n $.
The classification of finite group schemes over arbitrary ground schemes has been achieved in the case where the rank of $ G $ is a prime number (cf. [2]). The case where $ G $ is a commutative finite group scheme and $ S $ is the spectrum of a field of characteristic $ p $ is well known (see [1], [3], [7]).
References
| [1] | Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" Russian Math. Surveys , 18 (1963) pp. 1–80 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 3–90 |
| [2] | J. Tate, F. Oort, "Group schemes of prime order" Ann. Sci. Ecole Norm. Sup. , 3 (1970) pp. 1–21 |
| [3] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson (1970) |
| [4] | F. Oort, "Commutative group schemes" , Lect. notes in math. , 15 , Springer (1966) |
| [5] | S. Shatz, "Cohomology of Artinian group schemes over local fields" Ann. of Math. , 79 (1964) pp. 411–449 |
| [6] | B. Mazur, "Notes on étale cohomology of number fields" Ann. Sci. Ecole Norm. Sup. , 6 (1973) pp. 521–556 |
| [7] | H. Kraft, "Kommutative algebraische Gruppen und Ringe" , Springer (1975) |
Comments
For some spectacular applications of the results in [a1] see [a2], [a3].
References
| [a1] | M. Raynaud, "Schémas en groupes de type 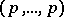 " Bull. Soc. Math. France , 102 (1974) pp. 241–280 " Bull. Soc. Math. France , 102 (1974) pp. 241–280 |
| [a2] | J.-M. Fontaine, "Il n'y a pas de variété abélienne sur 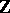 " Invent. Math. , 81 (1985) pp. 515–538 " Invent. Math. , 81 (1985) pp. 515–538 |
| [a3] | G. Faltings, "Endlichkeitssätze für abelsche Varietäten über Zahlkörpern" Invent. Math. , 73 (1983) pp. 349–366 (Erratum: Invent. Math 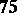 (1984), 381) (1984), 381) |
| [a4] | G. Cornell (ed.) J. Silverman (ed.) , Arithmetic geometry , Springer (1986) |
Finite group scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finite_group_scheme&oldid=15344