Finite-dimensional representation

A linear representation of a topological group in a finite-dimensional vector space. The theory of finite-dimensional representations is one of the most important and most developed parts of the representation theory of groups. An irreducible finite-dimensional representation is completely irreducible (see Schur lemma), but an operator-irreducible finite-dimensional representation can be reducible. A measurable finite-dimensional representation of a locally compact group locally coincides almost-everywhere with a continuous finite-dimensional representation. A bounded finite-dimensional representation of a locally compact group is equivalent to a unitary representation. A locally compact group having a faithful finite-dimensional representation is a Lie group [7].

A unitary finite-dimensional representation is a direct sum of irreducible unitary finite-dimensional representations. The intersection of the kernels of the continuous homomorphisms of a topological group 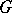coincides with the intersection of the kernels of the irreducible unitary finite-dimensional representations of 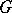; if this set contains only the identity of 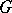, then there is a continuous monomorphism from 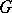into some compact group, and 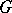is said to be imbeddable in a compact group, or to be a maximally almost-periodic group (a MAP-group). If 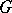is a MAP-group, then the family of matrix entries of irreducible finite-dimensional representations of 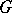separates points in 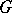. Commutative groups and compact groups are MAP-groups; a connected locally compact group is a MAP-group if and only if it is the direct product of a connected compact group and 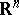(see [5]). A MAP-group can have infinite-dimensional irreducible unitary representations and need not be a group of type 1. 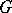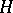Every continuous irreducible unitary representation of a locally compact group is finite-dimensional if and only if is a projective limit of finite extensions of groups of the form 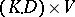, where 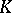, 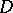and 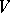are closed subgroups of 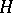such that 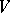is isomorphic to 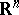, 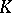is compact and 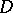is a discrete group that is central in 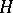[8]; a sufficient condition is that the quotient group of 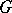by its centre be compact. Moreover, for many locally compact groups (in particular, for non-compact simple Lie groups), the only irreducible unitary finite-dimensional representation is the trivial representation.

Non-unitary finite-dimensional representations of topological groups have been classified (up to equivalence) only for special groups; in particular, for 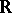and 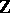, where the problem of describing finite-dimensional representations is solved by reducing matrices to Jordan form, and — in the case of 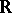— is related to the theory of ordinary differential equations with constant coefficients, in that the solution space of such an equation is a finite-dimensional invariant subspace of the regular representation of 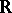in the space of continuous functions on 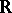. In addition, the finite-dimensional representations of connected semi-simple Lie groups are known. More precisely, these are direct sums of irreducible finite-dimensional representations that can be described as follows. If 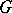is a semi-simple complex Lie group and 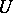is a maximal compact subgroup, then every continuous irreducible unitary representation 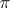of 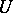in a space 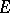can be extended: 1) to an irreducible representation 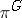of in 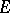whose matrix entries are analytic functions on 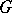; and 2) to an irreducible representation 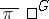of 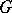whose matrix entries are complex conjugates of analytic functions on 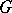; 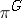and 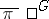are determined uniquely by 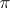. 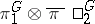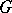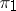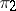The tensor product is an irreducible finite-dimensional representation of for arbitrary irreducible unitary finite-dimensional representations and of 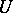, and every irreducible finite-dimensional representation of 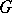is equivalent to a representation of the form 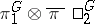. 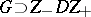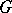A description of the finite-dimensional representations of a simply-connected connected complex semi-simple Lie group can also be given in terms of the exponentials of finite-dimensional representations of its Lie algebra, and also by using the Gauss decomposition of : Let 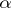be a continuous function on 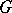such that 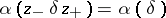for all 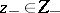, , 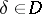, 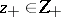and suppose that the linear hull 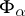of the functions 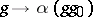, , 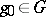is finite-dimensional; then the formula 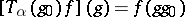, , 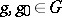, 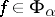defines an irreducible finite-dimensional representation of 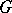, and all irreducible finite-dimensional representations of 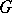can be obtained in this way. If 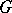is a real semi-simple Lie group having complex form 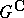, then every irreducible finite-dimensional representation of 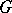is the restriction to 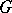of some unique irreducible finite-dimensional representation of 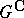whose matrix entries are analytic on 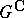(so that the theory of finite-dimensional representations of semi-simple connected Lie groups reduces essentially to that of compact Lie groups). A finite-dimensional representation of an arbitrary Lie group is real analytic; if 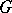is a simply-connected Lie group, then there is a one-to-one correspondence between the finite-dimensional representations of 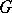and of its Lie algebras (associating to a representation of the Lie group its differential; the inverse mapping associates to a representation of the Lie algebra its exponential). However, the classification of finite-dimensional representations of arbitrary Lie groups is far from being completely solved (1988), even for the special cases of 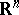, , 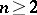and 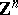, 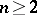(see [6]). On the other hand, the irreducible finite-dimensional representations 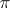of a connected Lie group 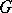are known [2]: They have the form 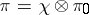, where 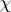is a one-dimensional representation of 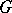(that is, essentially of its commutative quotient group by the commutator subgroup), and 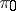is a finite-dimensional representation of the semi-simple quotient group of 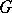by the maximal connected solvable normal subgroup of 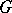(see Levi–Mal'tsev decomposition).

References

[1]	A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)
[2]	D.P. Zhelobenko, "Compact Lie groups and representations" , Amer. Math. Soc. (1973) (Translated from Russian)
[3]	M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian)
[4]	J. Dixmier, "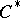 algebras" , North-Holland (1977) (Translated from French)
[5]	A. Weil, "l'Intégration dans les groupes topologiques et ses applications" , Hermann (1940)
[6]	I.M. Gel'fand, V.A. Ponomarev, "Remarks on the classification of a pair of commuting linear transformations in a finite-dimensional space" Funct. Anal. Appl. , 3 : 4 (1969) pp. 325–326 Funktsional. Anal. i Prilozhen. , 3 : 4 (1969) pp. 81–82
[7]	V.M. Glushkov, "The structure of locally compact groups and Hilbert's fifth problem" Transl. Amer. Math. Soc. , 15 (1960) pp. 55–93 Uspekhi Mat. Nauk , 12 : 2 (1957) pp. 3–41
[8]	A.I. Shtern, "Locally bicompact groups with finite-dimensional irreducible representations" Math. USSR Sb. , 19 : 1 (1973) pp. 85–94 Mat. Sb. , 90 : 1 (1973) pp. 86–95

References

[a1]	J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972)