Fine topology
in potential theory
The weakest topology in which all superharmonic functions on 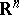 are continuous. Objects related to the fine topology are described as "fine" , "finely" , etc.
are continuous. Objects related to the fine topology are described as "fine" , "finely" , etc.
The notion of fine topology is closely connected with that of a thin set (cf. also Thinness of a set). The fine topology is stronger that the usual Euclidean topology on 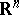 , i.e. every Euclidean-open set is finely open. A fine neighbourhood of a point
, i.e. every Euclidean-open set is finely open. A fine neighbourhood of a point  is a set
is a set 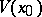 such that
such that 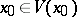 and such that the complement
and such that the complement 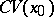 is a thin set at
is a thin set at  . The finely-open sets are unions of pre-images under mappings by superharmonic functions of the extended real line
. The finely-open sets are unions of pre-images under mappings by superharmonic functions of the extended real line  and of intervals of the form
and of intervals of the form 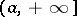 ,
, 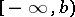 ,
, 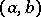 ,
, 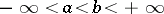 . Every superharmonic function on an open set
. Every superharmonic function on an open set 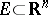 is finely continuous on
is finely continuous on 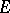 . A set
. A set 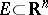 is thin at a point
is thin at a point  if and only if
if and only if 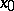 is a finely-isolated point of
is a finely-isolated point of 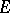 .
.
Let 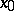 be a fine-limit point of
be a fine-limit point of 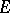 , that is,
, that is, 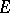 is not thin at
is not thin at 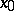 , and let
, and let 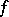 be a function defined on
be a function defined on 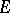 . The number
. The number  is called the fine limit of
is called the fine limit of 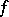 at
at 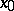 if for every neighbourhood
if for every neighbourhood 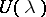 of
of 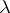 in
in 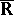 there exists a fine neighbourhood
there exists a fine neighbourhood 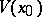 of
of 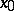 such that
such that
 |
If 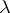 is the fine limit of
is the fine limit of 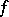 at
at 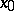 , then there exists a fine neighbourhood
, then there exists a fine neighbourhood 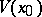 such that
such that 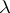 is an ordinary limit at
is an ordinary limit at 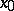 of the restriction
of the restriction 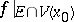 (Cartan's theorem).
(Cartan's theorem).
Let 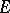 be a closed set, thin at a point
be a closed set, thin at a point 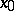 , and let
, and let  be a superharmonic function defined on
be a superharmonic function defined on 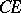 in a neighbourhood of
in a neighbourhood of 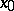 . Then
. Then 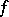 has a fine limit
has a fine limit  at
at 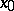 .
.
A fine topology has also been constructed in axiomatic potential theory (cf. [3]).
References
| [1] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
| [2] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [3] | M. Brélot, "Lectures on potential theory" , Tata Inst. (1960) |
Comments
A potential theory for finely-harmonic and finely-hyperharmonic functions is developed in [a1]. See also [a2].
References
| [a1] | B. Fuglede, "Finely harmonic functions" , Springer (1972) |
| [a2] | J. Lukeš, J. Malý, L. Zajíček, "Fine topology methods in real analysis and potential theory" , Springer (1986) |
Fine topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fine_topology&oldid=19006