Final object
terminal object, of a category
A concept formalizing the categorical property of a one-point set. An object  in a category
in a category  is called final if for every object
is called final if for every object  in
in  the set
the set  consists of a single morphism. A final object is also called a right null object of
consists of a single morphism. A final object is also called a right null object of  . A left null or initial object of a category is defined in the dual way.
. A left null or initial object of a category is defined in the dual way.
In the category of sets the final objects are just the one-point sets. In any category with null objects the final objects are the null objects. Other examples of final objects arise in various categories of diagrams, where the concept of a final object is essentially equivalent to that of the limit of a diagram. For example, suppose that  and let
and let  be the category of left equalizers of the pair
be the category of left equalizers of the pair  ; in other words, the objects of
; in other words, the objects of  are morphisms
are morphisms  for which
for which 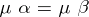 , and morphisms in
, and morphisms in 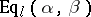 are morphisms
are morphisms  for which
for which 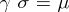 . A final object in
. A final object in 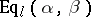 is a kernel of the pair of morphisms
is a kernel of the pair of morphisms 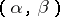 (cf. Kernel of a morphism in a category).
(cf. Kernel of a morphism in a category).
Comments
The set 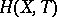 is, by definition, the set of morphisms
is, by definition, the set of morphisms 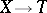 . Note that any two final objects of a category are (canonically) isomorphic, and so are two initial objects.
. Note that any two final objects of a category are (canonically) isomorphic, and so are two initial objects.
References
| [a1] | J. Adámek, "Theory of mathematical structures" , Reidel (1983) |
| [a2] | B. Mitchell, "Theory of categories" , Acad. Press (1965) pp. 4 |
Final object. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Final_object&oldid=13638