Filtered algebra
An algebra 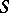 in which there are distinguished subspaces
in which there are distinguished subspaces 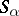 , indexed by the elements of a totally ordered group
, indexed by the elements of a totally ordered group 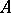 (most often
(most often  is the additive group of integers
is the additive group of integers 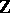 ), such that
), such that 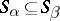 for
for 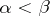 and
and  (an increasing filtration). Sometimes one considers the case where
(an increasing filtration). Sometimes one considers the case where 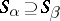 for
for 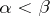 (a decreasing filtration), but it reduces to the preceding case by reversing the order in
(a decreasing filtration), but it reduces to the preceding case by reversing the order in 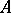 . With each filtered algebra
. With each filtered algebra 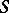 one associates the graded algebra
one associates the graded algebra
 |
where 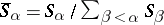 (if
(if 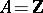 , then
, then 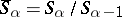 ), and the product of the elements
), and the product of the elements 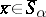 and
and 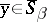 is defined by the formula
is defined by the formula 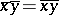 , where
, where  and
and 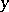 are representatives of the cosets
are representatives of the cosets 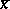 and
and 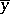 , and
, and 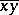 is the coset of
is the coset of 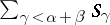 generated by
generated by 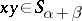 . If some multilinear identity is satisfied in
. If some multilinear identity is satisfied in 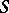 (for example, commutativity, associativity, or the Jacobi identity), then it is also satisfied in
(for example, commutativity, associativity, or the Jacobi identity), then it is also satisfied in 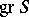 .
.
Examples.
1) Let 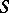 be a Clifford algebra and let
be a Clifford algebra and let 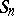 ,
, 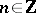 , be the collection of elements that can be represented in the form of (non-commutative) polynomials of degree
, be the collection of elements that can be represented in the form of (non-commutative) polynomials of degree 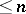 in the generators. One obtains an increasing
in the generators. One obtains an increasing 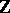 -filtration of
-filtration of 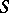 in which
in which  for
for 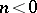 . The associated graded algebra is the exterior algebra with the same number of generators.
. The associated graded algebra is the exterior algebra with the same number of generators.
2) In the universal enveloping algebra of a Lie algebra one can define an increasing 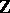 -filtration in the same way as in the preceding example. By the Birkhoff–Witt theorem, the associated graded algebra is the polynomial algebra.
-filtration in the same way as in the preceding example. By the Birkhoff–Witt theorem, the associated graded algebra is the polynomial algebra.
Filtered algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Filtered_algebra&oldid=12513